https://github.com/RainPPR/whk/edit/main/docs/math/sequence.md
数列 一堆手误的公式错误,欢迎指出!
下文中重要公式,均用 \(\boxed{}\) 框出来。
数列基础 数列 是由数字组成的有序序列,数列中的每一个数都叫做这个数列的项 。
项数 有限的数列成为有限数列 ,项数无穷多的成为无穷数列 。
排在第一位的数称为这个数列的首项 ,有限数列的最后一个数成为这个数列的末项 。
注意:无穷数列只有首项,没有末项。
对于数列,更严谨的定义,考虑最一般的复数,下文再说。
无穷数列 一个 \((a:\mathbb N\to\mathbb C)\) 的函数被称为无穷数列 。
可记为 \(\{a_i\}_{i\in\mathbb N}\) 或 \((a_i)_{i\in\mathbb N}\) 或 \(\langle a_i\rangle_{i\in\mathbb N}\) 。
一个数列 \(a\) 的第 \(i\) 项,通常记为 \(a(i)\) ,简记为 \(a_i\) 。
有限数列 若 \(I_n=\{1,2,\dots,n\}\) ,则一个 \((a:I_n\to\mathbb C)\) 的函数被称为有限数列 。
可记为 \(\{a_i\}_{i=1}^n\) 或 \((a_i)_{i=1}^n\) 或 \(\langle a_i\rangle_{i=1}^n\) 。
同时,也可以将 \(0\) 作为数列的首项,类似的。
单调性 对于 \(\forall n\in\mathbb Z^*\) ,
一般的表示方法 列举法 例如,
\[ a=\langle1,2,4,8,16\rangle \]
对于无穷数列很不好用。
图像法 数列是离散的,因此数列的图像是一个散点图。
一般这个不好用。
通项公式 定义,表示 \(n\) 和 \(a_n\) 的关系的公式,叫做 \(a\) 的通项公式 。
把数列看成函数的形式,
\[ a_n=f(n) \]
数列对应函数的解析式,被称为数列的通项公式。
例如,
\[ a_n=2^n \]
递推公式 定义,表示 \(a_n\) 和 \(a_n\) 的前一或前几项的关系的公式,叫做 \(a\) 的递推公式 。
例如,
\[ a_{n+1}=a_n+2 \]
特殊的,如果要根据递推公式确定一个数列,还需要知道数列的任意一项。
一般会表示数列的首项,例如,
\[ a_1=1 \]
如果一个数列只跟其前面的 \(k\) 项有关,其中 \(k\) 是满足这个条件的最小正整数,
那么称这个数列的阶数为 \(k\) ,即这个数列是一个 \(k\) 阶数列。
级数 数列中各个项的和称为级数 ,具体的,
一个数列 \(a_i\,(i\in\mathbb N)\) 的级数是另外一个数列 \(s_i\,(i\in\mathbb N)\) ,具有以下特性:
\(s_0=a_0\) ,\(s_n=s_{n-1}+a_n\,(\forall n\in\mathbb Z^*)\) 一般会将 \(\{s_i\}_{i\in\mathbb N}\) 写为,
\[ \sum _{i=0}^na_i \]
甚至更直观的 \(a_0+a_1+\dots +a_n\) 来凸显级数源于求和的直观概念。
对于从 \(1\) 开始的数列,同理,一般直接使用求和符号简记为,
\[ s_i=\sum_{i=1}^na_i \]
数列和函数 容易发现,数列,
\[ a_n=f(n) \]
其级数,即为 \(f\) 函数的积分,
\[ s_n=g(n) \]
其差分,即为 \(f\) 函数的微分,
\[ d_n=k(n) \]
只不过,函数一般是连续的,而数列一般是离散的。
等差数列 在等差数列中,任何相邻两项的差相等,该差值称为公差 \(d\) 。
具体的,可以表示为,
\[ a_n=d+qn \]
的,都是等差数列。
上式中,公差为 \(d\) ,首项 \(a_1=d+q\) 。
若 \(d>0\) ,等差数列为一个严格单调递增数列。 若 \(d<0\) ,等差数列为一个严格单调递减数列。 特殊的,若 \(d=0\) ,等差数列退化为一个常数列。 递推公式 形如,
\[ \boxed{a_{n+1}=a_n+d,(n\in\mathbb Z^*)} \]
或者记为,
\[ a_{n+1}-a_n=d \]
即公差的定义式。
通项公式 形如,
\[ \boxed{a_n=a_1+(n-1)d} \]
即,角标减一,等于公差个数。
或者对于从 \(0\) 开始的数列,
\[ a_n=a_0+nd \]
前面的一项即为首项,其与公差需为给定的确定的数。
性质 除了上述几条,
给定任意两项 \(a_n,a_m\) ,则公差,
\[ \boxed{d={a_n-a_m\over n-m}} \]
在等差数列中,前项与后项和为该项两倍,具体的,
\[ \begin{aligned} a_{n-1}+a_{n+1}&=a_n-d+a_n+d\\ &=2a_n \end{aligned} \]
从另一个角度看,等差数列中的任意一项,是其前项和后项的算术平均:
\[ a_n={a_{n-1}+a_{n+1}\over2} \]
对于正整数 \(m,n,p,q\) ,若 \(m+n=p+q\) ,则,
\[ \boxed{a_m+a_n=a_p+a_q} \]
或者简化一下,
\[ \boxed{a_m+a_n=a_{m-k}+a_{n+k}} \]
据此,有,
\[ \boxed{a_{n-k}+a_{n+k}=2a_n} \]
对于 \(a_{n-k},a_n,a_{n+k}\) 有意义。据此,同理,
\[ a_n={a_{n-k}+a_{n+k}\over2} \]
若 \(\langle a_n\rangle\) 为一个等差数列,则,
\(\langle b+a_n\rangle\) :为一个等差数列;\(\langle b\times a_n\rangle\) :为一个等差数列;\(\langle b^{a_n}\rangle\) :为一个等比数列(见下); 项数公式 给定等差数列首项 \(a_1\) 及公差 \(d\) ,有项 \(a_k\) ,则,
\[ \begin{aligned} a_k=a_1+(k-1)d\\ k-1={a_k-a_1\over d}\\ \boxed{k={a_k-a_1\over d}+1} \end{aligned} \]
或对于 \(a_0\) ,
\[ \begin{aligned} a_k=a_0+kd\\ k={a_k-a_0\over d}\\ \end{aligned} \]
另外的,函数思想,有,
\[ \begin{aligned} a_n=f(n)\\ n=g(a_n) \end{aligned} \]
即 \(f,g\) 互为反函数,这个可以用于求多种数列。
求和公式 一般考虑,
\[ S_i=\sum_{i=1}^na_i \]
有常用公式,
\[ S_n-S_{n-1}=a_n \]
考虑求解出,求和公式的封闭形式,
\[ \begin{aligned} S_n&=a_1+(a_1+d)+(a_1+2d)+\dots+[a_1+(n-1)d]\\ &=na_1+d[1+2+3+\dots(n-1)]\\ &=na_1+dT_{n-1} \end{aligned} \]
而对于,
\[ T_n=1+2+3+\dots+n \]
我们首位配对,
\[ T_n=n+(n-1)+\dots+1 \]
两者相加,
\[ \begin{aligned} 2T_n=n(n+1)\\ T_n=n(n+1)/2 \end{aligned} \]
于是,
\[ \begin{aligned} S_n&=na_1+dT_{n-1}\\ &=\boxed{na_1+{n(n-1)\over2}d}\\ &={n\over2}[2a_1+(n-1)d]\\ &=\boxed{{n(a_1+a_n)\over2}} \end{aligned} \]
或者,对于原始公式直接首位配对,用上面的结论,也可以得出。
总结一下,一般写为,
\[ \boxed{S_n={[2a_1+(n-1)]d\over2}\cdot n={n(a_1+a_n)\over2}} \]
常用二次函数的思想:
\[ \boxed{S_n={d\over2}n^2+\left(a_1-{d\over2}\right)n} \]
据此,可以等差数列和的极点存在于,
\[ \boxed{n={d/2-a_1\over d}={1\over2}-{a_1\over d}} \]
我们发现,该函数图像过原点,因此我们定义,
\[ S_0=0 \]
同时,对于上面的式子,如果我们假设存在 \(a_0\) ,那么求和,
得出很重要的一个结论,任何一个二次函数,都可以表示为一个等差数列的级数。
等差数列和在中文教科书中常表达为:
一个等差数列的和,等于其首项与末项的和,乘以项数除以二。
等差中项 对于 \(a,b\) ,有 \(c\) 满足,
\[ c-a=b-c \]
即,
\[ c={a+b\over2} \]
即算术平均数。
或者,若 \(\{a,b,c\}\) 为一个等差数列,那么
\[ b-a=c-b \]
一般写为,
\[ a+c=2b \]
可以用这个来判断一个三项数列是否为等差数列。
例题,对于等差数列 \(\{a,b,c\}\) ,证明,
\[ \left\{{1\over\sqrt b+\sqrt c},{1\over\sqrt c+\sqrt a},{1\over\sqrt a+\sqrt b}\right\} \]
也是一个等差数列。
暴力展开,
\[ {2\over\sqrt c+\sqrt a}={1\over\sqrt b+\sqrt c}+{1\over\sqrt a+\sqrt b}\\ {2\over\sqrt c+\sqrt a}={2\sqrt b+\sqrt a+\sqrt c\over b+\sqrt b(\sqrt a+\sqrt c)+\sqrt{ac}}\\ 2b+2\sqrt{ac}+2\sqrt b(\sqrt a+\sqrt c)=2\sqrt b(\sqrt a+\sqrt c)+a+c+\sqrt ac\\ a+c=2b \]
对于等差数列 \(\{a,b,c\}\) 成立。Q.E.D.
或者,观察到原式中,分母都是根号的形式,考虑分母有理化,
\[ {2\over\sqrt c+\sqrt a}={1\over\sqrt b+\sqrt c}+{1\over\sqrt a+\sqrt b}\\ {2(\sqrt c-\sqrt a)\over2d}={\sqrt c-\sqrt b\over d}+{\sqrt b-\sqrt a\over d} \]
显然成立。
累加法 最简单的,形如,
\[ a_n=a_{n-1}+f(n) \]
都可以使用累加法,具体的,
\[ \begin{aligned} a_n&=a_{n-1}+f(n)\\ a_{n-1}&=a_{n-2}+f(n-1)\\ &\dots\\ a_3&=a_2+f(3)\\ a_2&=a_1+f(2) \end{aligned} \]
上述所有式子相加,得
\[ a_n=a_1+f(2)+f(2)+\dots+f(n) \]
多阶等差数列 容易发现,我们对于公差求前缀和,可以得到一个普通等差数列。
那么,我们对于普通等差数列再求和,就可以得到二阶等差数列。
具体的,定义常数为零阶等差数列,普通等差数列为一阶等差数列。
容易发现,若 \(\{a_i\}\) 为一阶等差数列,\(\{b_i\}\) 同样,那么 \(\{a_ib_i\}\) 为一个二阶等差数列。
根据定义,对于一个二阶等差数列,其相邻两项的差为一个一阶等差数列,相邻两项差的相邻两项差为一个常数。
等比数列 在等比数列中,任何相邻两项的比例相等,该比值称为公比 \(q\) 。
具体的,可以表示为,
\[ a=pq^n \]
的,都是等比数列。
上式中,公比为 \(q\) ,首项 \(a_1=pq\) 。
递推公式 形如,
\[ \boxed{a_{n+1}=qa_n,\,(n\in\mathbb Z^*,q\neq0)} \]
或者记为,
\[ \boxed{q={a_{n+1}\over a_n}} \]
即公比的定义式。
易知此式中,\(a_n\neq0\) ,为了方便,我们一般规定 \(q\neq0\) 。
通项公式 形如,
\[ \boxed{a_n=a_1q^{n-1}} \]
换句话说,任意一个等比数列 \(\{a_n\}\) 都可以写为,
\[ \{a,aq,aq^2,\dots aq^{n-1}\} \]
即,角标减一,等于公比幂次。
性质 除了上述几条,
在等比数列中,前项与后项积为该项平方,具体的,
\[ \begin{aligned} a_{n-1}\times a_{n+1}&=aq^{n-2}aq^{n}\\ &=a^2q^{2n-2}\\ &=(aq^{n-1})^2\\ &=a_n^2 \end{aligned} \]
对于正整数 \(m,n,p,q\) ,若 \(m+n=p+q\) ,则,
\[ \boxed{a_m\cdot a_n=a_p\cdot a_q} \]
或者简化一下,
\[ \boxed{a_m\cdot a_n=a_{m-k}\cdot a_{n+k}} \]
据此,有,
\[ \boxed{a_{n-k}\cdot a_{n+k}=a_n^2} \]
还有一些和上面等比数列类似的操作的结论,
但是因为正负号的问题,不具体写出,可以根据上述平方的公式推导。
若 \(\langle a_n\rangle\) 为一个等比数列,则,
\(\langle b+a_n\rangle\) :为一个等比数列;\(\langle b\times a_n\rangle\) :为一个等比数列;\(\langle \log_ba_n\rangle\) :为一个等差数列(见上); 求和公式 等差数列中给出的公式依然成立,
\[ S_n-S_{n-1}=a_n \]
实际上,这个对于任意数列都成立。
考虑求解出,等比数列求和公式的封闭形式,
\[ \begin{aligned} S_n&=a_1+a_1q+a_1q^2+\dots+a_1q^{n-1}\\ &=a_1(1+q+q^2+\dots+q^{n-1}) \end{aligned} \]
注意到后面的是经典的分解因式,
\[ \boxed{S_n=a_1\cdot{q^n-1\over q-1},\,(q\neq 1)} \]
或者,错位相减,
\[ \begin{aligned} qS_n-S_n=a_1q^n-a_1\\ S_n=a_1\cdot{q^n-1\over q-1},\,(q\neq 1) \end{aligned} \]
同时,若 \(q=1\) ,数列退化为常数列,
\[ \boxed{S_n=na_1,\,(q=1)} \]
等比中项 对于 \(a,b\) ,有 \(c\) 满足,
\[ {b\over c}={c\over a} \]
即,
\[ c=\pm\sqrt{ab} \]
取其中的正数,即几何平均数。
累乘法 和累加法类似的,
\[ a_n=a_{n-1}f(n) \]
累乘法,即
\[ \begin{aligned} a_n&=a_{n-1}f(n)\\ a_{n-1}&=a_{n-2}f(n-1)\\ &\dots\\ a_3&=a_2f(3)\\ a_2&=a_1f(2) \end{aligned} \]
上述所有式子相乘,得
\[ a_n=a_1f(2)f(3)\dots f(n) \]
裂项 经典例题 有性质,
\[ \boxed{{1\over n(n+1)}={1\over n}-{1\over n+1}} \]
可以求解,形如
\[ S={1\over1\times2}+{1\over2\times3}+\dots+{1\over n(n+1)} \]
的问题。
同时,易证,
\[ \boxed{{1\over n(n+k)}={1\over k}\left({1\over k}-{1\over n+k}\right)} \]
注意,此时裂项一定要找准剩下的。
我们可以分别写出括号内的正数、负数。
以 \(k=2\) 为例,
\[ S={1\over1\times3}+{1\over2\times4}+\dots+{1\over n(n+2)} \]
化简,
\[ 2S={1\over1}-{1\over3}+{1\over2}-{1\over4}+\dots+{1\over n}-{1\over n+2} \]
列出正负,
\[ \begin{aligned} +&:{1\over1},{1\over2},{1\over3},\dots,{1\over n-1},{1\over n}\\ -&:{1\over3},{1\over4},{1\over5},\dots,{1\over n+1},{1\over n+2} \end{aligned} \]
容易发现,
\[ 2S=1+{1\over2}-{1\over n+1}-{1\over n-2} \]
或者用求和符号简单的表示,下文再说。
整式裂项 有公式,
\[ \boxed{n(n+1)={1\over3}\Big[n(n+1)(n+2)-(n-1)n(n+1)\Big]} \]
于是,例题,
\[ S=1\times2+2\times3+3\times4+\dots+n(n+1) \]
化简,
\[ 3S=1\times2\times3-0\times1\times2+\dots+n(n+1)(n+2)-(n-1)n(n+1) \]
得,
\[ S={n(n+1)(n+2)\over3} \]
利用上述等式,注意到,
\[ n^2=n(n+1)-n \]
于是,
\[ \boxed{1^2+2^2+\dots+n^2=S-{n(n+1)\over2}={n(n+1)(2n+1)\over6}} \]
或者用求和符号简单的表示,下文再说。
共轭根式 形如,
\[ \sqrt a+\sqrt b,\sqrt a-\sqrt b \]
的,称为共轭根式。
容易证明,
\[ (\sqrt a-\sqrt b)\cdot(\sqrt a+\sqrt b)=a-b\;(a,b\ge0) \]
于是,有裂项,
\[ {1\over\sqrt a+\sqrt b}={\sqrt a-\sqrt b\over a-b} \]
以及,
\[ {1\over\sqrt a-\sqrt b}={\sqrt a+\sqrt b\over a-b} \]
阶乘 定义,
\[ \boxed{n!=1\times2\times3\times\dots\times(n-1)\times n} \]
称为阶乘,有,
\[ \boxed{n\cdot n!=(n+1)!-n!} \]
还有组合数的,但是这里还没涉及到。
放缩 放缩基础 数列求和是一种精确的方法,当我们无法精确的计算的时候,就可以放缩来估计。
例如,估计
\[ S={1\over1^2}+{1\over2^2}+\dots+{1\over n^2} \]
的级别。
容易发现,
\[ {1\over n}-{1\over n-1}={1\over n(n+1)}<{1\over n^2}<{1\over n(n-1)}={1\over n-1}-{1\over n} \]
于是,我们可以以此估计。
我们把 \(1/1^2\) 保持不动,估计
\[ 1.5<S<2 \]
而为了提高精度,我们减少放缩的项数。
或者说,把 \(1/2^2,1/3^2\) 等直接计算,而不是放缩。
这就是放缩提高精度的方法:保留更多的项。
放缩进阶 引理一: $$ {\sqrt k\over k^2}={1\over k^{3/2}}<2\left({1\over\sqrt{k-1}}-{1\over\sqrt k}\right) $$
通用方法 例题,求解通项:
\[ a_n=2a_{n-1}+1\;(n\ge2),a_1=1 \]
下面将对于这一类的问题,总结三个通用方法。
方法一:数学归纳法 尝试证明,
\[ a_n=2^n-1 \]
容易发现,
\[ a_1=2^1-1=1 \]
假设对于 \(n=k,k\in\mathbb N^*\) 成立,
\[ a_k=2^k-1 \]
尝试证明对于 \(n=k+1\) 也成立,
\[ a_{k+1}=2a_k+1=2^{k+1}-2+1=2^{k+1}-1 \]
于是,该通项公式对于任意 \(n\in\mathbb N^*\) 成立。
方法二:变形法 容易发现,递推公式两边同时加一,
\[ a_n+1=2a_{n-1}+2 \]
另,
\[ b_n=a_n+1 \]
上式即为,
\[ b_n=2b_{n-1},b_1=2 \]
那么这是一个等比数列,易得,
\[ b_n=2^n \]
那么,根据关系,
\[ a_n=b_n-1=2^n-1 \]
Q.E.D.
考虑推广这一类问题 ,形如,
\[ a_n=pa_{n-1}+q \]
我们两边同时加一个数,设为 \(x\) ,
\[ a_n+x=pa_{n-1}+q+x \]
记新数列,
\[ b_n=a_n+x,a_n=b_n-x \]
原数列,
\[ b_n=p(b_{n-1}-x)+q+x=pb_{n-1}+q-(p-1)x \]
另右侧常数项为零,于是,
\[ \boxed{x={q\over p-1}} \]
即,对于原数列,加上这个数,即可转化为普通的等比数列。
方法三:变形累加 容易得出,下面的式子不断乘二,
\[ \begin{aligned} a_n=2a_{n-1}+1\\ 2a_{n-1}=4a_{n-1}+2\\ 4a_{n=2}=8a_{n-2}+4\\ \dots\\ 2^{n-3}a_3=2^{n-2}a_2+2^{n-3}\\ 2^{n-2}a_2=2^{n-1}a_1+2^{n-2} \end{aligned} \]
上述式子相加,
\[ a_n=2^{n-1}a_1+2^{n-2}+2^{n-3}+\dots+4+2+1 \]
因为 \(a_1=1\) ,
\[ a_n=2^n-1 \]
Q.E.D.
考虑推广这一类问题 ,形如,
\[ a_n=pa_{n-1}+q \]
我们还可以等式两边同除 \(p^n\) ,得
\[ \boxed{{a_n\over p^n}={a_{n-1}\over p^{n-1}}+{q\over p^n}} \]
设新的数列,
\[ b_n={a_n\over p^n} \]
原数列形如,
\[ b_n=b_{n-1}+{q\over p^n} \]
对 \(b\) 数列进行累加法,可以得出,
\[ b_n={a_1\over p}+{q\over p^2}+{q\over p^3}+\dots+{q\over p^n} \]
右边为等比数列,即,
\[ b_n={a_1\over p}+{q\over p^n}\cdot{p^n-1\over p-1}-{q\over p} \]
两边同时乘 \(p^n\) ,
\[ \boxed{a_n=(a_1-q)p^{n-1}+{q\over p-1}(p^n-1)} \]
即通用公式。
同时,若 \(q=f(n)\) ,依然可以用这个方法来做。
基础例题 求下列数列的通项公式。
例题一 求:\(a_n=2a_{n-1}+3\,(n\ge2),a_1=1\) 。
因为 \(q/(p-1)=3\) ,等式两边同时加三,
\[ a_n+3=2a_{n-1}+6=2^{n+1}\\ a_n=2^{n+1}-3 \]
注意到当 \(n=1,a_1=1\) 满足该式,因此,
\[ a_n=2^{n+1}-3 \]
例题二 求:\(a_n=a_{n-1}+n\,(n\ge2),a_1=1\) 。
注意到,
\[ a_n=a_{n-1}+n\\ a_{n-1}=a{n-2}+n-1\\ \dots\\ a_2=a_1+2=1+2 \]
上式相加,得,
\[ a_n=1+2+3+\dots+n-1+n={n(n+1)\over2} \]
注意到当 \(n=1,a_1=1\) 满足该式,因此,
\[ a_n={n(n+1)\over2} \]
例题三 求:\(a_n=2a_{n-1}+n\,(n\ge2),a_1=1\) 。
等式两边同时除以 \(2^n\) ,得,
\[ {a_n\over2^n}={a_{n-1}\over2^{n-1}}+{n\over2^n} \]
记 \(b_n=a_n/2^n\) ,
\[ b_n=b_{n-1}+n/2^n\\ b_{n-1}=b_{n-2}+(n-1)/2^{n-1}\\ \dots\\ b_2=b_1+1/2\\ b_1=1/2 \]
上式相加,得,
\[ b_n={n\over2^n}+{n-1\over2^{n-1}}+\dots+{1\over2}+{1\over2} \]
注意到分母为二的幂次的形式,等式乘二,
\[ 2b_n={n\over2^{n-1}}+{n-1\over2^{n-2}}+\dots+1+1 \]
下式减上式,得,
\[ \begin{aligned} b_n&=-{n\over2^n}+{1\over2^{n-1}}+{1\over2^{n-2}}+\dots+{1\over2^1}+1\\ &={1\over2^{n-1}}\left(1+2+\dots+2^{n-1}\right)-{n\over2^n}\\ &={2^n-1\over2^{n-1}}-{n\over2^n}=2-{2+n\over2^n} \end{aligned} \]
带入原式,
\[ a_n=2^nb_n=2^{n+1}-2-n \]
注意到当 \(n=1,a_1=1\) 满足该式,因此,
\[ a_n=2^{n+1}-2-n \]
例题四 求:\(a_n=2a_{n-1}+n^2\,(n\ge2),a_1=1\) 。
等式两边同时除以 \(2^n\) ,得,
\[ {a_n\over2^n}={a_{n-1}\over2^{n-1}}+{n^2\over2^n} \]
记,
\[ b_n=a_n/2^n,a_n=2^nb_n \]
则,
\[ b_n=b_{n-1}+{n^2\over2^n},b_1={a_1\over2^1}={1\over2}={1^2\over2^1} \]
得,
\[ b_n={1^2\over2^1}+{2^2\over2^2}+{3^2\over2^3}+{4^2\over2^4}+\dots+{(n-1)^2\over2^{n-1}}+{n^2\over2^n} \]
两边同时乘二,得,
\[ 2b_n=1+{2^2\over2^1}+{3^2\over2^2}+{4^2\over2^3}+\dots+{(n-1)^2\over2^{n-2}}+{n^2\over2^{n-1}} \]
下式减上式,得,
\[ b_n=1-{n^2\over2^n}+{2^2-1^2\over2^1}+{3^2-2^2\over2^2}+{4^2-3^2\over2^3}+\dots+{(n-1)^2-(n-2)^2\over2^{n-2}}+{n^2-(n-1)^2\over2^{n-1}} \]
注意到,
\[ n^2-(n-1)^2=n^2-n^2-1+2n=2n-1 \]
于是,记,
\[ \begin{aligned} c_n&={2^2-1^2\over2^1}+{3^2-2^2\over2^2}+{4^2-3^2\over2^3}+\dots+{(n-1)^2-(n-2)^2\over2^{n-2}}+{n^2-(n-1)^2\over2^{n-1}}\\ &={2\times2-1\over2^1}+{2\times3-1\over2^2}+{2\times4-1\over2^3}+\dots+{2(n-1)-1\over2^{n-2}}+{2n-1\over2^{n-1}} \end{aligned} \]
即,
\[ b_n=1-{n^2\over2^n}+c_n \]
下式两边同时乘二,得,
\[ 2c_n=3+{2\times3-1\over2^1}+{2\times4-1\over2^2}+\dots+{2(n-1)-1\over2^{n-3}}+{2n-1\over2^{n-2}}\\ \]
与原式相减,得,
\[ \begin{aligned} c_n&=3-{2n-1\over2^{n-1}}+{2\over2^1}+{2\over2^2}+\dots+{2\over2^{n-3}}+{2\over2^{n-2}}\\ &=3-{2n-1\over2^{n-1}}+{1\over2^0}+{1\over2^1}+\dots+{1\over2^{n-4}}+{1\over2^{n-3}}\\ &=3-{2n-1\over2^{n-1}}+{1\over2^{n-3}}(1+2+2^2+\dots+2^{n-3})\\ &=3-{2n-1\over2^{n-1}}+{2^{n-2}-1\over2^{n-3}}\\ &=5-{2n-1\over2^{n-1}}-{1\over2^{n-3}} \end{aligned} \]
于是,
\[ b_n=1-{n^2\over2^n}+c_n=6-{n^2\over2^n}-{2n-1\over2^{n-1}}-{1\over2^{n-3}} \]
于是,
\[ a_n=2^nb_n=3\times2^{n+1}-n^2-4n-6 \]
注意到当 \(n=1,a_1=1\) 满足该式,因此,
\[ a_n=3\times2^{n+1}-n^2-4n-6 \]
线性递推 概念 对于 \(k\) 阶线性递推式,\(a_n\) 仅与 \(n\) 前面的 \(k\) 项有关。
对于常系数齐次线性递推,形如,
\[ \boxed{a_n=\sum_{i=1}^kf_i\times a_{n-i}} \]
拓展:对于常系数非齐次线性递推,形如,
\[ a_n=P(n)+\sum_{i=1}^kf_i\times a_{n-i} \]
其中 \(P(x)\) 是一个 \(m\) 次多项式。
特征方程和特征根 形如,
\[ a_n=xa_{n-1}+ya_{n-2} \]
其特征方程可以表示为,
\[ \boxed{q^2=xq+y}\\ q^2-xq-y=0 \]
推导:
设有 \(q,t\) 满足,
\[ a_n-qa_{n-1}=t(a_{n-1}-qa_{n-2})\\ a_n=(q+t)a_{n-1}-qta_{n-2} \]
则,
\[ \begin{cases} x=q+t\\ y=-qt \end{cases} \]
得,
\[ q=x-t=x+y/q\\ t=x-q=-y/q\\ q^2=xq+y \]
或者用微分方程的思想,
\[ q^n=xa^{n-1}+ya^{n-2} \]
注意到 \(a^{n-2}\neq0\) ,化简得,
\[ q^2=xq+y \]
易解得,
\[ \boxed{q_{1,2}={x\pm\sqrt{x^2+4y}\over2}} \]
其中,\(q_{1,2}\) 称为原线性递推式的特征根。
拓展到高阶线性递推式,对于,
\[ a_n=\sum_{i=1}^kf_i\times a_{n-i} \]
其特征方程为,
\[ q^k=\sum_{i=1}^kf_i\times q^{k-i} \]
特征根与通项公式 我们记递推式
\[ a_n=xa_{n-1}+y_{n-2} \]
的两个特征根分别为,\(q_1,q_2\) ,那么
通项公式,\(a_n\) 一定可以表示为,
\[ \boxed{a_n=\alpha q_1^n+\beta q_2^n} \]
特殊的,如果 \(q_1=q_2=q\) ,
\[ a_n=(\alpha+\beta)q^n \]
其中,还可以进一步表示,
\[ \alpha+\beta=\lambda n+\mu \]
带入原式,
\[ \boxed{a_n=(\lambda n+\mu)q^n} \]
对于更高阶的,把 \(n\) 前面多加几项 \(n^2,n^3,\dots\) 即可。
特殊的,若,
\[ a_2/a_1=q \]
那么,原式继续退化,形如,
\[ \boxed{a_n=kq^n} \]
可以根据上面的结论,将一个常系数齐次线性递推式,直接化为等差、等比数列。
同时,容易发现 \(k_1,k_2\) 一定对于任意 \(n\) 成立,因此带入特殊值,
\[ \boxed{\begin{aligned} a_1=\alpha q_1+\beta q_2\\ a_2=\alpha q_1^2+\beta q_2^2 \end{aligned}} \]
容易发现,只有 \(k_1,k_2\) 为未知量,可以直接解出来,得到通项公式。
拓展到高阶,理论类似,实际难算。
基础例题 例题一:斐波那契数列 有递推式,
\[ \begin{cases} a_1=a_2=1\\ a_n=a_{n-1}+a_{n-2}\;(n>2) \end{cases} \]
有特征方程,
\[ q^2=q+1 \]
解得,
\[ q_{1,2}={1\pm\sqrt5\over2} \]
即,
\[ a_n=\lambda_1\left({1+\sqrt5\over2}\right)^n+\lambda_2\left({1-\sqrt5\over2}\right)^n \]
带入 \(a_1=a_2=1\) ,
\[ \def\qa#1{{a#1\sqrt5\over2}} \begin{aligned} a_1&=\lambda_1\qa++\lambda_2\qa-\\ a_2&=\lambda_1\left(\qa+\right)^2+\lambda_2\left(\qa-\right)^2 \end{aligned} \]
解得,
\[ \begin{aligned} \lambda_1&={1\over\sqrt5}\\ \lambda_2&=-{1\over\sqrt5} \end{aligned} \]
即,斐波那契数列通项公式,
\[ \boxed{a_n={1\over\sqrt5}\left[\left({1+\sqrt5\over2}\right)^n-\left({1-\sqrt5\over2}\right)^n\right]} \]
同时,我们有更简便的方法,考虑到,
\[ a_n=\lambda_1q_1^n+\lambda_2q_2^n \]
也可以表示为,
\[ a_n=\lambda_1q_1^{n-1}+\lambda_2q_2^{n-1} \]
于是,我们带入 \(a_1,a_2\) ,
\[ \begin{cases} a_1=\lambda_1+\lambda_2\\ a_2=\lambda_1q_1+\lambda_2q_2 \end{cases} \]
会更方便解方程一点。
本题中,
\[ \left\{\begin{aligned} \lambda_1+\lambda_2&=1\\ \lambda_1{1+\sqrt5\over2}+\lambda_2{1-\sqrt5\over2}&=1 \end{aligned}\right. \]
解得,
\[ \left\{\begin{aligned} \lambda_1&={1+\sqrt5\over2\sqrt5}\\ \lambda_2&=-{1-\sqrt5\over2\sqrt5} \end{aligned}\right. \]
得,
\[ \begin{aligned} a_n&={1+\sqrt5\over2\sqrt5}\left({1+\sqrt5\over2}\right)^{n-1}-{1-\sqrt5\over2\sqrt5}\left({1-\sqrt5\over2}\right)^{n-1}\\ &={1\over\sqrt5}\left[\left({1+\sqrt5\over2}\right)^n-\left({1-\sqrt5\over2}\right)^n\right] \end{aligned} \]
例题二 求:
\[ a_{n+1}=3a_n-2a_{n-1} \]
对于任意 \(a_1,a_2\) 的通项公式。
容易发现,这是一个二阶的常系数齐次线性递推式,考虑求出特征根,
\[ q^2=3q-2\\ q_1=1,q_2=2 \]
于是,有
\[ a_n=x+y\cdot2^n \]
对于,解方程
\[ \begin{cases} a_1=x+2y\\ a_2=x+4y \end{cases} \]
解得,
\[ \left\{\begin{aligned} x&=2a_1-a_2\\ y&={a_2-a_1\over2} \end{aligned}\right. \]
于是,
\[ a_n=2a_1-a_2+(a_2-a_1)2^{n-1} \]
例题三 求:
\[ a_{n+1}=6a_n-9a_{n-1} \]
对于任意 \(a_1,a_2\) 的通项公式。
容易发现,这是一个二阶的常系数齐次线性递推式,考虑求出特征根,
\[ q^2=6q-9\\ q_1=q_2=3 \]
于是,有,
\[ a_n=(xn+y)3^n \]
带入,
\[ \begin{aligned} a_1&=3x+3y\\ a_2&=18x+9y \end{aligned} \]
那么,
\[ \begin{aligned} x&={a_2-3a_1\over9}\\ y&={6a_1-a_2\over9} \end{aligned} \]
于是,
\[ a_n=[(a_2-3a_1)n+6a_1-a_2]3^{n-2} \]
例题四 对于,
\[ a_n=4a_{n-1}-3a_{n-2}+1,a_1=1,a_2=2 \]
注意到特征方程
\[ x^2=4x-3 \]
其特征根为,
\[ x_1=1,x_2=3 \]
我们考虑最原始的算法,两边同时减去 \(3a_{n-1}\) ,
\[ a_n-3a_{n-1}=a_{n-1}-3a_{n-2}+1 \]
设,
\[ b_n=a_n-3a_{n-1} \]
则,
\[ b_n=b_{n-1}+1,b_2=a_2-3a_1=-1 \]
于是,
\[ b_n=n-3 \]
则,
\[ a_n=3a_{n-1}+n+3 \]
两边同时除以 \(3^n\) 即可,暴力求解即可。
但是还有更方便的算法,注意到,
\[ a_n=4a_{n-1}-3a_{n-2}+1\\ a_{n+1}=4a_n-3a_{n-1}+1 \]
下式减上式,
\[ a_{n+1}-a_n=4a_n-3a_{n-1}-4a_{n-1}+3a_{n-2} \]
即,
\[ a_{n+1}=5a_n-7a_{n-1}+3a_{n-2} \]
于是,我们把一个非齐次的递推式,转化为了一个齐次的,特征根
\[ q^3=5q^2-7q+3 \]
首先,注意到 \(q=1\) 为一个可行解,于是,
\[ q^3-5q^2+7q-3=(q-1)(q^2-4q+3)=(q-1)^2(q-3)=0 \]
即,
\[ q_1=q_2=1,q_3=3 \]
于是,
\[ a_n=\beta3^{n-1}+\lambda n+\mu \]
根据原递推式,得出,
\[ a_3=4a_2-3a_1+1=6 \]
于是,列出方程,
\[ \begin{cases} 1=\beta+\lambda+\mu\\ 2=3\beta+2\lambda+\mu\\ 6=9\beta+3\lambda+\mu \end{cases} \]
考虑解方程,具体的,
\[ \begin{cases} 2\beta+\lambda=1\\ 6\beta+\lambda=4 \end{cases} \]
解得,
\[ \left\{\begin{aligned} \beta={3\over4}\\ \lambda=-{1\over2}\\ \mu={3\over4} \end{aligned}\right. \]
即,
\[ a_n={3^n\over4}-{1\over2}n+{3\over4} \]
经检验,\(a_1=1,a_2=2,a_3=6\) ,符合题意,故,略。
类似,若特征方程无解,那么数列为一个周期数列,手模即可。
注意到,利用这个低阶化为高阶的方法,可以避免很多前面的题中类似的大量计算。
对于这一类的问题,我们把各种变形,转化为只需要解特征方程就可以的问题。
例题五 求通项公式,
\[ a_{n+1}=4a_n-3a_{n-1}+n\,(n\ge2),a_1=1,a_2=2 \]
考虑和上一题类似的做法,
\[ a_n=4a_{n-1}-3a_{n-2}+n-1 \]
上式减下式,
\[ a_{n+1}=5a_n-7a_{n-1}+3a_{n-2}+1 \]
继续运用上一题的思路,
\[ a_n=5a_{n-1}-7a_{n-2}+3a_{n-3}+1 \]
上式减下式,得,
\[ a_{n+1}=6a_n-12a_{n-1}+10a_{n-2}-3a_{n-3} \]
解出特征方程,
\[ q_1=q_2=q_3=1,q_4=3 \]
设通项公式,
\[ a_n=a3^{n-1}+b(n-1)^2+c(n-1)+d \]
带入即可,步骤略。
例题六 已知数列 \(\{a\},\{b\}\) 满足,
\[ a_1=2,b_1=1\\ \begin{aligned} a_{n+1}&=5a_n+3b_n+7\\ b_{n+1}&=3a_n+5b_n \end{aligned} \]
对于 \(n\in\mathbb N\) ,求 \(\{a\}\) 解析式。
容易发现,我们可以利用上式,用 \(a_{n+1},a_n\) 表示 \(b_n\) 。
然后带入下式,即可求得 \(a_n\) 的递推公式。
但是这么做很复杂,考虑原递推公式有什么优秀的结构。
容易发现,\(5,3,3,5\) 存在有一种优美的形态,
于是,考虑两式做和、做差。
\[ \begin{cases} a_{n+1}+b_{n+1}=8a_n+8b_n+7\\ a_{n+1}-b_{n+1}=2a_n-2b_n+7 \end{cases} \]
设,
\[ c_n=a_n+b_n\\ d_n=a_n-b_n \]
于是,
\[ \begin{cases} c_{n+1}=8c_n+7\\ d_{n+1}=2d_n+7 \end{cases} \]
然后用通用方法,
\[ c_{n+1}+1=8c_n+8=8(c_n+1)\\ c_n=8^{n-1}(c_1+1)-1=4\times8^{n-1}-1 \]
同理,
\[ d_{n+1}+7=2d_n+14=2(d_n+7)\\ d_n=2^{n-1}(d_1+7)-7=8\times2^{n-1}-7 \]
则,
\[ a_n={c_n+d_n\over2}=2\times8^{n-1}+2^{n+1}-4 \]
经检验,\(a_1=2\) ,符合题意,故,
\[ a_n=2\times8^{n-1}+2^{n+1}-4 \]
例题七 数列 \(\{a\}\) 满足,
\[ a_1=1,a_2=2,a_{n+2}=6a_{n+1}-a_n \]
则,下列说法中,正确的是,
A. 数列 \(\{a_{n+1}^2-a_na_{n+2}\}\) 是常数数列。
B. 数列 \(\{8a_na_{n+1}-7\}\) 的各项为平方数。
C. 数列 \(\{4a_na_{n+1}-7\}\) 的各项为平方数。
D. 任意 \(a_n\) 除以 \(9\) 的余数为 \(1\) 或 \(2\) 。
对于 A 选项,我们递推式两边同时乘上 \(a_n\) ,
\[ a_na_{n+2}=6a_na_{n+1}-a_n^2 \]
则,
\[ a_{n+1}^2-a_na_{n+2}=a_{n+1}^2+a_n^2-6a_na_{n+1} \]
同理,
\[ a_n^2-a_{n-1}a_{n+1}=a_n^2+a_{n-1}^2-6a_{n-1}a_n \]
两式右面相等,则,
\[ a_{n+1}^2-6a_na_{n+1}=a_{n-1}^2-6a_{n-1}a_n\\ a_{n+1}(a_{n+1}-6a_n)=a_{n-1}(a_{n-1}-6a_n)\\ -a_{n+1}a_{n-1}=-a_{n-1}a_{n+1} \]
显然成立,因此,数列
\[ \{a_{n+1}^2-a_na_{n+2}\} \]
是常数数列。
对于 D 选项,容易发现,
\[ a_1\equiv1\pmod 9\\ a_2\equiv2\pmod 9\\ a_3\equiv2\pmod 9\\ a_4\equiv1\pmod 9\\ a_5\equiv4\pmod 9 \]
在 \(a_5\) 出现问题,故命题不成立。
对于 BC 选项,由 A 选项知,
\[ a_{n+1}^2-a_na_{n+2}=a_{n+1}^2+a_n^2-6a_na_{n+1}=-7 \]
则,
\[ 6a_na_{n+1}-7=a_{n+1}^2+a_n^2 \]
两边同时,
\[ \pm2a_na_{n+1} \]
都可以使右边变为平方数,因此 BC 均成立。
故选:ABC。
极限 函数极限 极限的概念比较复杂,我们多方面的考虑。
若函数 \(f(x)\) 在 \(x_0\) 附近有定义,且存在有极限 \(L\) ,那么,
对于任意 \(\varepsilon>0\) ,一定存在 \(\delta>0\) ,使得当,
\[ 0<|x-x_0|<\delta \]
时,总有,
\[ |f(x)-L|<\varepsilon \]
则称 \(L\) 是函数在 \(x_0\) 的极限 ,记为,
\[ \lim_{x\to x_0}f(x)=L \]
特殊的,若对于 \(x>x_0\) (\(x-x_0<\delta\) )满足上式,
则称函数在 \(x_0\) 处存在右极限 ,表示为:
\[ \lim_{x\to x_0^+}f(x)=L \]
同样的,若对于 \(x<x_0\) (\(x_0-x<\delta\) )满足上式,
则称函数在 \(x_0\) 处存在左极限 ,表示为:
\[ \lim_{x\to x_0^-}f(x)=L \]
比较这三个定义我们会发现:
要想存在极限,那么必须同时存在相等的左极限和右极限。
数列极限 数列极限的定义和函数的不大一样,
对于任意 \(\varepsilon>0\) ,都存在 \(N\in\mathbb N^*\) ,使得对于任意 \(n>N\) ,
\[ |a_n-L|<\varepsilon \]
则称数列 \(a\) 收敛于 \(L\) ,记为,
\[ \lim_{n\to\infty}a_n=L \]
或,
\[ a_n\to a \]
用逻辑符号表示,
\[ (\forall\varepsilon>0)(\exist N\in\mathbb N^+)(\forall n\in\mathbb N)[(n>N)\Rightarrow(|a_n-L|<\varepsilon)] \]
直观的讲,即无论误差范围 \(\varepsilon\) 多小,从某项 \(a_n\) 开始,每一项与 \(L\) 的差距都小于 \(\varepsilon\) 。
或者,更直观的,当数列的下标越来越大的时候,数列的值也就越接近那个特殊值。
若不存在这样的数,则称该数列是发散 的。
常见的极限 从这里开始,一般只讨论数列极限。
\[ \boxed{\lim_{x\to\infty}{1\over x^n}=0,n>0}\tag a \]
\[ \boxed{\lim_{x\to\infty}{1\over a^n}=0,|a|>1}\tag b \]
\[ \boxed{\lim_{x\to\infty}r^n=0,|r|<1}\tag c \]
\[ \boxed{\lim_{x\to0^+}{1\over x}=+\infty}\tag d \]
\[ \boxed{\lim_{x\to0^-}{1\over x}=-\infty}\tag e \]
特殊的,对于数列 \(a_n=n\) ,
当 \(n\to+\infty\) 时,\(a_n\to+\infty\) ,这种无界数列 ,一般说其不存在极限。
同样,除了常数数列,其他的波动数列、周期数列,一般都不存在极限。
其中一个判断数列是否收敛的定理,称为单调收敛定理 ,和实数完备性相关:
单调有界数列必收敛(有上界的单调递增数列,或是有下界的单调递减数列)。
同时,判断数列是否收敛,还存在两边夹定理 ,
若两数列存在极限,那么其夹的数列存在极限,数学表示,
若 \(\lim\limits_{n\to\infty}a_n=\lim\limits_{n\to\infty}b_n=L\) ,且 \(a_n\le c_n\le b_n\) ,则 \(\lim\limits_{n\to\infty}c_n=L\) 。
例如,
\[ 0<{1\over\sqrt{n^2+1}}<{1\over n} \]
且左右极限都是 \(0\) ,因此中间也收敛于 \(0\) 。
极限的性质 唯一性 :若数列 \(\{a_n\}_{n\in\mathbb N}\) 存在极限,则极限是唯一的。
有界性 :如果一个实数数列无界,则这个实数数列一定发散。
若数列 \(\{a_n\}_{n\in\mathbb N}\) 存在极限,那么一定存在 \(M>0\) ,使得所有 \(|a_n|\le M\) 。
注意到,并不是数列有界就一定存在极限,例如 \(a_n=(-1)^{n}\) 。
保序性 :若两数列 \(\{a_n\}_{n\in\mathbb N},\{b_n\}_{n\in\mathbb N}\) 分别收敛于 \(A,B\) ,则,
\[ (\exist N\in\mathbb N)[(A>B)\wedge(n>N)\Rightarrow(a_n>b_n)] \]
极限也存在四则运算:
\[ \boxed{\lim_{n\to\infty}(a_n\pm b_n)=\lim_{n\to\infty}a_n\pm \lim_{n\to\infty}b_n}\tag1 \]
\[ \boxed{\lim_{n\to\infty}xa_n=x\lim_{n\to\infty}a_n}\tag2 \]
由 \((1)(2)\) 可得极限的线性性 ,
\[ \boxed{\lim_{n\to\infty}(xa_n+yb_n)=x\lim_{n\to\infty}a_n+y\lim_{n\to\infty}b_n}\tag3 \]
另外,极限也存在乘法和除法,
\[ \boxed{\lim_{n\to\infty}(a_nb_n)=\lim_{n\to\infty}a_n\times\lim_{n\to\infty}b_n}\tag4 \]
\[ \tag5\boxed{\lim_{n\to\infty}\left({a_n\over b_n}\right)={\lim_{n\to\infty}a_n\over\lim_{n\to\infty}b_n}} \]
注意到,被除数不能为零。
同时,如果要进行以上所有操作,都需要保证每一步的数列极限存在。
这样子,有一个性质,
\[ \lim_{n\to\infty}{a_1x^{c_1}+a_2x^{c_2}+\dots\over b_1x^{c_1}+b_2x^{c_2}+\dots}={a_1\over b_1},c_1>c_2>\dots \]
即,最高次项系数之比。
极限例题 存在极限的组 \[ \lim_{n\to\infty}{1\over4^n}=0 \]
\[ \lim_{n\to\infty}{2\over n}+{1\over n^2}=\lim_{n\to\infty}{2\over n}+\lim_{n\to\infty}{1\over n^2}=0 \]
\[ \lim_{n\to\infty}{1\over n}-{2\over n^2}+3=\lim_{n\to\infty}{1\over n}-\lim_{n\to\infty}{2\over n^2}+3=3 \]
\[ \lim_{n\to\infty}{2+(1/3)^n\over(1/3)^n-5}={\lim_{n\to\infty}2+(1/3)^n\over\lim_{n\to\infty}(1/3)^n-5}={2+\lim_{n\to\infty}(1/3)^n\over\lim_{n\to\infty}(1/3)^n-5}=-{2\over5} \]
注意在做每一步变形的时候,只有存在极限才能操作。
\[ \lim_{n\to\infty}{3n+1\over2n+2}={3\over2} \]
这里有很多种做法,例如,
\[ \lim_{n\to\infty}{3n+1\over2n+2}=\lim_{n\to\infty}{3+1/n\over2+2/n}={\lim_{n\to\infty}3+1/n\over\lim_{n\to\infty}2+2/n}={3\over2} \]
\[ \lim_{n\to\infty}{3n+1\over2n+2}=\lim_{n\to\infty}{3(2n+2)/2-2\over2n+2}={3\over2}-\lim_{n\to\infty}{2\over2n+2}={3\over2} \]
或者,当 \(n\to\infty\) 时,
\[ 3n+1\sim3n,2n+2\sim2n \]
\[ {3n+1\over2n+2}\to{3n\over2n}={3\over2} \]
不存在极限的组 \[ a_n=\sqrt n \]
注意到,
\[ n\to\infty,\sqrt n\to\infty \]
当趋近于正无穷时,一般认为不存在极限。
\[ a_n=n-{1\over n} \]
注意到,
\[ n\to\infty,1/n\to0 \]
故,
\[ a_n\to\infty \]
同样不存在极限。
例题一 \[ a_n={1\over\sqrt{n^2+n}} \]
容易发现,
\[ 0<{1\over\sqrt {n^2+n}}<{1\over n} \]
且,
\[ \lim_{n\to\infty}{1\over n}=0 \]
根据两边夹定理,
\[ \lim_{n\to\infty}{1\over\sqrt{n^2+n}}=0 \]
例题二 \[ a_n={\sin n\over n} \]
容易发现,
\[ -{1\over n}\le{\sin n\over n}\le{1\over n} \]
且,
\[ \lim_{n\to\infty}-{1\over n}=\lim_{n\to\infty}{1\over n}=0 \]
因此,
\[ \lim_{n\to\infty}{\sin n\over n}=0 \]
例题三 \[ a_n=\sqrt[n]2 \]
注意到,
\[ \sqrt[n]2>0 \]
而且,
\[ \sqrt[n]2>\sqrt[n+1]2 \]
证明:
\[ (\sqrt[n]2)^{n(n+1)}>(\sqrt[n+1]2)^{n(n+1)}\\ 2^{n+1}>2^n \]
即,递减有下界,有极限。
设,
\[ a_n=\sqrt[n]2\\ c_n=a_n-1 \]
那么,
\[ (c_n+1)^n=2 \]
用二项式定理展开,
\[ \sum_{k=0}^n{n\choose k}c_n^k=2 \]
展开前两项,
\[ 1+nc_n<(c_n+1)^n=2\\ c_n<{1\over n} \]
即,
\[ 1<a_n=c_n+1<{1\over n}+1 \]
根据两边夹定理,
\[ \lim_{n\to\infty}a_n=1 \]
例题四 \[ b_n=\sqrt[n]n \]
的极限。
类似上一题的似乎,设,
\[ d_n=b_n-1\\ b_n=d_n+1\\ n=(d_n+1)^n \]
展开,
\[ 1+nd_n+{n(n+1)\over2}d_n^2+\dots=n \]
考虑到右面的 \(n\) 级别比较大,我们选用一三两项,
\[ n>1+{n(n+1)\over2}d_n^2\\ n-1>{n(n+1)\over2}d_n^2\\ {n\over2}d_n^2<1\\ d_n^2<{2\over n} \]
又因为,
\[ d_n>1 \]
两边夹,得出,
\[ \lim_{n\to\infty}b_n=\lim_{n\to\infty}d_n+1=1 \]
例题五:数学直觉做法 有数列,
\[ a_1=1,a_{n+1}=a_n+{1\over\sqrt[2n]{a_n}} \]
判断 \(a\) 是否单调,是否有界。
我们充分发扬人类智慧:
\[ a_1=1,a_2=2,\dots \]
观察原式,容易得出,
\[ a_n\neq0,{1\over\sqrt[2n]{a_n}}\neq0 \]
那么,
\[ a_{n+1}>a_n \]
而且不取等,那么一定是严格单调递增且无界的。
例题六:初中重造组 求数列,
\[ a_0=1+2021^{-1}\\ a_n=(1+2021^{-2^n})a_{n-1} \]
的极限。
注意到两边取极限,会约去,因此不能不动点法(大雾)。
注意到幂运算的右结合性,
\[ 2021^{-2^n}=(2021^{-2})^n=\left({1\over2021}\right)^{2^{n}} \]
我们记,
\[ x=2021^{-1} \]
那么,原式化简为,
\[ a_0=1+x\\ a_n=(1+x^{2^n})a_{n-1} \]
考虑累乘法,很自然,
\[ a_n=(1+x)(1+x^2)(1+x^4)+\dots+(1+x^{2^n}) \]
好好好,我们回归初中出现过的经典探究题,
\[ (1-x)(1+x)=1-x^2\\ (1-x^2)(1+x^2)=1-x^4\\ \dots\\ (1-x^{2^n})(1+x^{2^n})=1-\left(x^{2^n}\right)^2=1-x^{2^n\times2}=1-x^{2^{n+1}} \]
于是,原式两边同乘 \(1-x\) ,得,
\[ (1-x)a_n=1-x^{2^{n+1}}\\ a_n={1-x^{2^{n+1}}\over1-x} \]
考虑极限,
\[ \lim_{n\to\infty}a_n={1-\lim_{n\to\infty}x^{2^{n+1}}\over1-x} \]
我们知道,
\[ n\to\infty\Rightarrow2^{n+1}\to\infty\Rightarrow x^{2^{n+1}}\to0,\because|x|<1 \]
因此,
\[ \lim_{n\to\infty}a_n={1\over1-x}={2021\over2020} \]
不动点法 不动点 对于函数 \(f\) ,若 \(x\) 满足,
\[ f(x)=x \]
这个 \(x\) 称为这个函数的不动点 ,或定点,是被这个函数映射到其自身一个点。
例如:
\[ f(x)=x^{2}-3x+4 \]
的不动点为,
\[ x=f(x)\\ x^2-4x+4=0\\ (x-2)^2=0 \]
即函数 \(f\) 的不动点为 \(2\) ,因为 \(f(2)=2\) 。
不是每一个函数都具有不动点,例如定义在实数上的函数 \(f(x)=x+1\) 就没有不动点。
因为对于任意的实数, \(x\) 永远不会等于 \(x+1\) 。
用画图的话来说,不动点意味着点 \((x,f(x))\) 在直线 \(y=x\) 上,即图像存在交点。
上例 \(f(x)=x+1\) 的情况是,这个函数的图像与那根直线是一对平行线。
在函数的有限次迭代之后回到相同值的点叫做周期点;不动点是周期等于 1 的周期点。
不动点和数列 如果数列递推公式形如,
\[ a_{n+1}=f(a_n) \]
那么,\(f\) 称为迭代函数 (生成函数 ),则和上文一样,
\[ x=f(x) \]
的方程,称为不动点方程 。
当我们解出一个不动点 \(x\) ,等式两边同时减去 \(x\) ,
\[ a_{n+1}-x=f(a_n)-x \]
左右都等于零,因此右面一定有因式,
\[ a_n-x \]
这个过程称为不动点改造 。
那么,左右就存在相同的结构,
\[ b_n=a_n-x \]
往往可以进而推导一些性质。
不动点法求极限 有数列形如,
\[ a_n=f(a_{n-1}) \]
假设这个数列存在极限,记为 \(a\) ,那么对两边同时取极限,
\[ \lim_{n\to\infty}a_n=\lim_{n\to\infty}f(a_{n-1}) \]
一般默认 \(f\) 函数是光滑的,那么,
\[ \lim_{n\to\infty}f(a_{n-1})=f(\lim_{n\to\infty}a_{n-1}) \]
即,
\[ a=f(a) \]
解出这个解,那么如果存在极限,极限一定是这个方程的解中的一个。
原理为,只有当数列收敛到不动点,才能存在极限;不然也不会存在极限。
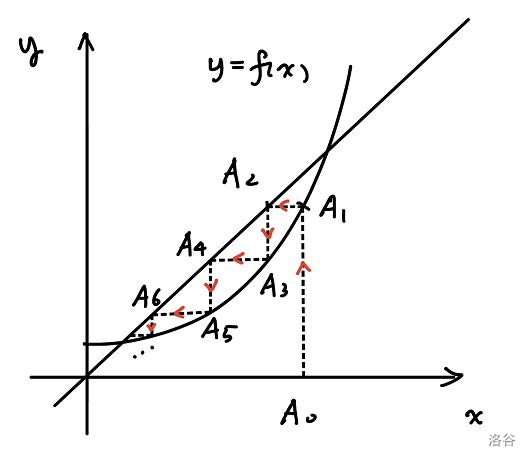
数列迭代:蛛网工作法 我们延续上面的观点,尝试使用一些新奇的技巧,
我们想要把数列 \(a_n\to a_{n+1}\) 这个过程直观的表示出来,我们知道,
\[ f(a_n)=a_{n+1} \]
容易想到,我们在平面内做出 \(f(x)\) 的图像,那么这上面的点,
\[ Q(a_n,f(a_n))=(a_n,a_{n+1}) \]
就表示了一个递推的过程。
然后考虑数列运作的趋势是什么样的,显然我们只考虑递增和递减,
\(f(a_n)>a_n\) ,数列在此处递增,对应点在 \(y=x\) 图像上方;\(f(a_n)<a_n\) ,数列在此处递减,对应点在 \(y=x\) 图像下方。 于是,我们考虑在平面内再做出 \(y=x\) 的图像,那么数列的趋势符合上文。
具体的,做点,
\[ A_1(a_1,f(a_1))=(a_1,a_2) \]
过 \(A_1\) 做 \(x\) 轴平行线,交 \(y=x\) 于,
\[ A_2(a_2,a_2) \]
过 \(A_2\) 做 \(y\) 轴平行线,交 \(y=f(x)\) 于,
\[ A_3(a_2,f(a_2))=(a_2,a_3) \]
以此类推,形如,
我们知道,按照顺序在 \(y=f(x)\) 图像上的点,对应原数列。
根据这个图像,我们还能知道不动点 \(x=f(x)\) 其实是这两个图像的交点。
于是,如果我们这么做下去,能推到不动点附近,那么函数收敛。
与上文类似,指数函数、幂函数的线性组合,一般都是光滑的,那么有,
若 \(|f'(x_0)|<1\) ,不动点 \(x_0\) 称为吸引不动点,数列迭代过程中会靠近吸引不动点。
若 \(|f'(x_0)|>1\) ,不动点 \(x_0\) 称为排斥不动点,数列迭代过程中会远离排斥不动点。
通项公式:例题 一次函数形 例题:有数列,
\[ a_1=1,a_n={1\over2}a_{n-1}+1 \]
求 \(a_n\) 的通项公式。
求出不动点 \(x\) ,满足,
\[ x={1\over2}x+1\\ x=2 \]
原式两边同时减二,
\[ a_n-2={1\over2}a_{n-1}-1={1\over2}(a_{n-1}-2) \]
因此,
\[ a_n-2={1\over2^{n-1}}(a_1-2)\\ a_n=-{1\over2^{n-1}}+2 \]
二次函数型(双解) 解,
\[ a_1=3,a_{n+1}={4a_n-2\over a_n+1} \]
求出不动点,
\[ x={4x-2\over x+1}\\ x^2+x=4x-2\\ x^2-3x+2=0\\ (x-2)(x-1)=0 \]
我们把两个不动点 \(2,1\) 分别减到递推式两边,
\[ a_{n+1}-2={2a_n-4\over a_n+1}\\ a_{n+1}-1={3a_n-3\over a_n+1} \]
化简,
\[ a_{n+1}-2={2(a_n-2)\over a_n+1}\\ a_{n+1}-1={3(a_n-1)\over a_n+1} \]
然后上下做比,
\[ {a_{n+1}-2\over a_{n+1}-1}={2\over3}\cdot{a_n-2\over a_n-1} \]
注意到是等比数列,因此,
\[ {a_n-2\over a_n-1}=\left({2\over3}\right)^{n-1}{a_1-2\over a_1-1}={1\over2}\left({2\over3}\right)^{n-1} \]
记后面的为 \(S_n\) ,则,
\[ {a_n-2\over a_n-1}=S_n\\ a_n-2=a_nS_n-S_n\\ (S_n-1)a_n=S_n-2\\ a_n={S_n-2\over S_n-1} \]
带入,得,
\[ a_n={(2/3)^{n-1}-4\over(2/3)^{n-1}-2}={2^{n-1}-4\cdot3^{n-1}\over2^{n-1}-2\cdot3^{n-1}} \]
二次函数型(单解) 解,
\[ a_1=5,a_{n+1}={3a_n-4\over a_n-1} \]
不动点,
\[ x^2-x=3x-4\\ x^2-4x-4=0\\ x=2 \]
只有一个解,我们两边减去,
\[ a_{n+1}-2={a_n-2\over a_n-1} \]
注意到两个分子形式相同,我们两边取倒数,
\[ {1\over a_{n+1}-2}={a_n-1\over a_n-2}=1+{1\over a_n-2} \]
为等比数列,
\[ {1\over a_n-2}={1\over a_1-1}+(n-1)=n-{2\over3} \]
两边再取倒数,
\[ a_n-2={1\over n-2/3}={3\over3n-2}\\ a_n={3\over3n-2}+2={6n-1\over3n-2} \]
二次函数型(无解) 解,
\[ a_1=2,a_n=1-{1\over a_{n-1}} \]
不动点,
\[ x=1-{1\over x}\\ x^2=x-1\\ x^2-x+1=0 \]
无解,因此该数列为周期数列,考虑,
\[ a_1=2\\ a_2=1/2\\ a_3=-1\\ a_4=2 \]
为 \(T=3\) 的周期数列,因此,
\[ a_n=\left\{\begin{aligned} 2&\quad\operatorname{if}n\equiv1\pmod3\\ 1/2&\quad\operatorname{if}n\equiv2\pmod3\\ -1&\quad\operatorname{if}n\equiv0\pmod3\\ \end{aligned}\right. \]
不动点解题技巧 适用于形如 \(a_{n+1}=f(a_n)\) ,
求解通项公式部分,求解不动点 \(x=f(x)\) 后,
【若为一次函数】:两边减去,构造等比;
【若为二次函数双解】:两边减去两个不动点,做比,构造等比;
【若为二次函数单解】:减去不动点,去倒数,通分,构造等差;
【若为二次函数无解】:为周期数列,手模即可。
例题 已知从 \(1\) 开始的数列,
\[ a_1=2,a_{n+1}=(\sqrt2-1)(a_n+2)\\ b_1=2,b_{n+1}={3b_n+4\over2b_n+3} \]
求证,
\[ \sqrt2<b_n\le a_{4n-3} \]
考虑直接求出通项公式,
对于数列 \(\{a_n\}\) ,不动点,
\[ x=(\sqrt2-1)(x+2)\\ x=(\sqrt2-1)x+2(\sqrt2-1)\\ (2-\sqrt2)x=2(\sqrt2-1)\\ x=(\sqrt2-1)(2+\sqrt2)\\ x=\sqrt2 \]
两边减去 \(\sqrt2\) ,
\[ a_{n+1}-\sqrt2=(\sqrt2-1)a_n+\sqrt2-2=(\sqrt2-1)(a_n-\sqrt2) \]
因此,
\[ a_n-\sqrt2=(\sqrt2-1)^{n-1}(a_1-\sqrt2)=(2-\sqrt2)(\sqrt2-1)^{n-1}\\ a_n=\sqrt2(\sqrt2-1)^n+\sqrt2 \]
对于数列 \(\{b_n\}\) ,不动点,
\[ 2x^2+3x=3x+4\\ x^2=2\\ x_{1,2}=\pm\sqrt2 \]
两边减去,
\[ b_{n+1}-\sqrt2={(3-2\sqrt2)(b_n-\sqrt2)\over2b_n+3}\\ b_{n+1}+\sqrt2={(3+2\sqrt2)(b_n+\sqrt2)\over2b_n+3} \]
做比,
\[ {b_{n+1}+\sqrt2\over b_{n+1}-\sqrt2}={3+2\sqrt2\over3-2\sqrt2}\cdot{b_n+\sqrt2\over b_n-\sqrt2} \]
注意到,
\[ {3+2\sqrt2\over3-2\sqrt2}={(\sqrt2+1)^2\over(\sqrt2-1)^2}=\left({\sqrt2+1\over\sqrt2-1}\right)^2 \]
于是,
\[ \begin{aligned} {b_n+\sqrt2\over b_n-\sqrt2}&=\left({\sqrt2+1\over\sqrt2-1}\right)^{2(n-1)}{b_1+\sqrt2\over b_1-\sqrt2}\\ &=\left({\sqrt2+1\over\sqrt2-1}\right)^{2n-2}{2+\sqrt2\over 2-\sqrt2}\\ &=\left({\sqrt2+1\over\sqrt2-1}\right)^{2n-2}{\sqrt2+1\over\sqrt2-1}\\ &=\left({\sqrt2+1\over\sqrt2-1}\right)^{2n-1}=x \end{aligned} \]
则,
\[ b_n+\sqrt2=xb_n-\sqrt2x\\ (x-1)b_n=\sqrt2(x+1)\\ b_n=\sqrt2{x+1\over x-1}=\sqrt2{(\sqrt2+1)^{2n-1}+(\sqrt2-1)^{2n-1}\over(\sqrt2+1)^{2n-1}-(\sqrt2-1)^{2n-1}} \]
考虑进一步化简,此时有两个形式,
\[ b_n=\sqrt2{(\sqrt2+1)^{4n-2}+1\over(\sqrt2+1)^{4n-2}-1}=\sqrt2{1+(\sqrt2-1)^{4n-2}\over1-(\sqrt2-1)^{4n-2}} \]
考虑证明给出的性质,
\[ \sqrt2<b_n\le a_{4n-3}=\sqrt2(\sqrt2-1)^{4n-3}+\sqrt2 \]
即,
\[ 1<{1+(\sqrt2-1)^{4n-2}\over1-(\sqrt2-1)^{4n-2}}\le(\sqrt2-1)^{4n-3}+1 \]
左侧显然,右侧,移项,
\[ {2(\sqrt2-1)^{4n-2}\over1-(\sqrt2-1)^{4n-2}}\le(\sqrt2-1)^{4n-3}\\ {2(\sqrt2-1)\over1-(\sqrt2-1)^{4n-2}}\le1\\ 2(\sqrt2-1)\le1-(\sqrt2-1)^{4n-2}\\ (\sqrt2-1)^{4n-2}\le3-2\sqrt2=(\sqrt2-1)^2\\ 4n-2\ge2,n\ge1 \]
显然成立。
三角换元初步 思路 我们复习一下再换元里面常用的恒等变换,
\[ \boxed{\cos2\theta=2\cos^2\theta-1}\tag1 \]
\[ \boxed{\tan2\theta={2\tan\theta\over1-\tan^2\theta}}\tag2 \]
\[ \boxed{\sin3\theta=3\sin\theta-4\sin^2\theta}\tag3 \]
\[ \boxed{\cos3\theta=4\cos^2\theta-3\cos\theta}\tag4 \]
注意到,除了正切函数,其他的函数值域都是 \([-1,1]\) (不指定定义域)。
因此,我们先需要证明函数值在一个区间内,然后利用上面的去换元。
例题 已知数列 \(\{a_n\}\) 满足,
\[ a_1={1\over2},a_{n+1}=a_n^2-2 \]
观察到右面类似余弦二倍角公式,考虑猜测 \(a_n\in[-2,2]\) 。
证明:考虑数学归纳,
\[ -2\le a_1={1\over2}\le2 \]
尝试,\(a_n\in[-2,2]\Rightarrow a_{n+1}\in[-2,2]\) 。
\[ a_{n-1}=a_n^2-2 \]
由于,
\[ a_n\in[-2,2]\Rightarrow a_n^2\in[0,4]\Rightarrow a_n^2-2\in[-2,2] \]
因此,注意到递推式右面的 \(2\) ,我们设,
\[ a_n=2\cos\theta_n \]
容易发现,
\[ a_{n+1}=a_n^2-2\\ 2\cos\theta_{n+1}=4\cos^2\theta_n-2\\ \cos\theta_{n+1}=2\cos^2\theta_n-1\\ \cos\theta_{n+1}=\cos2\theta_n \]
不妨令,
\[ \theta_{n+1}=2\theta_n \]
于是,通项公式,
\[ a_n=2\cos(2^{n-1}\theta) \]
考虑 \(\theta\) 是多少,
\[ a_1=2\cos\theta={1\over2}\\ \cos\theta={1\over4}\\ \theta=\arccos1/4 \]
即,
\[ a_n=2\cos\left(2^{n-1}\arccos{1\over4}\right) \]
跑题了 若,
\[ a_1=3, a_{n+1}=2a_n^2-1 \]
欸,三角换元,啊初项不行 QAQ
我们考虑另外一个满足此式的式子,另,
\[ a_n={k^x+k^{-x}\over2}=f(x) \]
其中 \(k\) 是任意变量,则,
\[ a_{n+1}=2a_n^2-1={k^{2x}+k^{-2x}\over2}=f(2x) \]
令,初项,
\[ a_1=f(t)={k^t+k^{-t}\over2}=3 \]
令,
\[ k^t=3+2\sqrt2,k^{-t}=3-2\sqrt2 \]
于是,
\[ a_2=f(2t)={k^{2t}+k^{-2t}\over2}\\ a_3=f(4t)={k^{4t}+k^{-4t}\over2}\\ \dots\\ a_n=f(2^{n-1}t)={k^{2^{n-1}t}+k^{-2^{n-1}t}\over2}={(k^t)^{2^{n-1}}+(k^{-t})^{2^{n-1}}\over2} \]
带入,得,
\[ a_n={(3+2\sqrt2)^{2^{n-1}}+(3-2\sqrt2)^{2^{n-1}}\over2} \]
这个东西就是(类似)双曲换元。
裂项和放缩 分式裂项 第一组:
\[ \boxed{{1\over n(n+1)}={1\over n}-{1\over n+1}} \]
推广,
\[ \boxed{{1\over n(n+k)}={1\over k}\left({1\over n}-{1\over n+k}\right)} \]
第二组:
\[ \boxed{{1\over n(n+1)(n+2)}={1\over2}\left[{1\over n(n+1)}-{1\over(n+1)(n+2)}\right]} \]
推广,
\[ \boxed{{1\over n(n+1)\dots (n+k)}={1\over k}\left[{1\over n\dots(n+k-1)}-{1\over(n+1)\dots(n+k)}\right]} \]
整式裂项 第一组,
\[ \boxed{n(n+1)={1\over3}[{\color{blue}n(n+1)}(n+2)-(n-1){\color{blue}n(n+1)}]} \]
推广,
\[ \boxed{n(n+1)\dots(n+m)={1\over m+2}[{\color{blue}n\dots}(n+m+1)-(n-1){\color{blue}\dots(n+m)}]} \]
根式裂项 第一组,
\[ \boxed{{1\over\sqrt{n+1}-\sqrt n}=\sqrt{n+1}+\sqrt n} \]
推广,
\[ \boxed{{1\over\sqrt{n+k}-\sqrt n}={\sqrt{n+k}+\sqrt n\over k}} \]
或者,
\[ \boxed{{1\over\sqrt a\pm\sqrt b}={\sqrt a\mp\sqrt b\over a\pm b}} \]
第二组,对于 \(0<\alpha<1\) ,
\[ \boxed{{1\over1-\alpha}\left[{1\over(n+1)^{\alpha-1}}-{1\over n^{\alpha-1}}\right]<{1\over n^\alpha}<{1\over1-\alpha}\left[{1\over n^{\alpha-1}}-{1\over(n-1)^{\alpha-1}}\right]},n\ge2 \]
例如,
\[ \begin{aligned} \alpha=1/2&\longrightarrow\boxed{2(\sqrt{n+1}-\sqrt n)<\sqrt n<2(\sqrt n-\sqrt{n-1})}\\ \alpha=1/3&\longrightarrow\boxed{{3\over2}\left(\sqrt[3]{(n+1)^2}-\sqrt[3]{n^2}\right)<{1\over\sqrt[3]n}<{3\over2}\left(\sqrt[3]{n^2}-\sqrt[3]{(n-1)^2}\right)} \end{aligned} \]
证明,
\[ \int_n^{n+1}{1\over x^\alpha}\mathrm dx<{1\over n^\alpha}<\int_{n-1}^n{1\over x^\alpha}\mathrm dx \]
由牛顿·莱布尼茨公式化简得上式。
另一组,
\[ \sqrt{2n+4}-\sqrt{2n+2}<{1\over\sqrt{2n+1}}<\sqrt{2n+1}-\sqrt{2n-1} \]
证明大体形如,
\[ {1\over\sqrt{2n+1}}<{1\over(\sqrt{2n+1}+\sqrt{2n-1})/2}=\sqrt{2n+1}-\sqrt{2n-1} \]
例题 简单例题 已知等差数列 \(\{a_n\}\) 满足,\(a_3=7,a_5+a_7=26\) ,
求 \(a_n\) 及其前 \(n\) 项和 \(S_n\) ; 令 \(b_n=1/(a_n^2-1)\) ,求其前 \(n\) 项和 \(T_n\) 。 易知,
\[ a_5+a_7=2a_6=26,a_6=13\\ d=(a_6-a_3)/(6-3)=2\\ a_1=a_3-2d=3 \]
于是,
\[ a_n=a_1+(n-1)d=3+2(n-1)=2n+1\\ S_n=n(a_1+a_n)/2=n^2+2n \]
那么,
\[ b_n={1\over a_n^2-1}={1\over 4n^2+4n}={1\over4}\cdot{1\over n(n+1)}={1\over 4}\left({1\over n}-{1\over n+1}\right) \]
那么,
\[ T_n=b_1+b_2+\dots+b_n={1\over4}\left({1\over1}-{1\over2}+{1\over2}-{1\over3}+\dots+{1\over n}-{1\over n+1}\right) \]
注意好配对,
\[ T_n={1\over4}\left(1-{1\over n+1}\right)={n\over 4n+4} \]
基础例题 已知数列 \(\{a_n\}\) 满足,
\[ a_1=1,a_2=1/4\\ a_{n+1}={(n-1)a_n\over n-a_n} \]
求证,对于任意 \(n\in\mathbb N^*\) ,
\[ \sum_{i=1}^na_i^2<{7\over6} \]
注意到递推公式并不是不动点的标准形式,但是,
发现如果把分母乘过去,\(n\) 的系数相同,会约去,因此,
设不动点 \(x\) ,
\[ x={(n-1)x\over n-x}\\ nx-x^2=nx-x\\ x^2-x=x(x-1)=0\\ x_1=0,x_2=1 \]
两边减去一,
\[ a_{n+1}-1={n(a_n-1)\over n-a_n} \]
与原式做比,
\[ {a_{n+1}\over a_{n+1}-1}={n-1\over n}\cdot{a_n\over a_n-1} \]
注意到左边系数的分母,两项相差了一,因此,
\[ n{a_{n+1}\over a_{n+1}-1}=(n-1){a_n\over a_n-1} \]
因此,
\[ (n-1){a_n\over a_n-1} \]
对于 \(n\ge2\) 为常数列,因此,
\[ (n-1){a_n\over a_n-1}={a_2\over a_2-1}=-{1\over3} \]
则,
\[ 1-a_n=(3n-3)a_n\\ (3n-2)a_n=1\\ a_n={1\over 3n-2} \]
尝试证明,
\[ S_n=\sum_{i=1}^na_i^2<{7\over6}\\ 1+{1\over 4^2}+{1\over 7^2}+{1\over 10^2}+\dots<{7\over6} \]
进行放缩,
注意到我们要把每一项放缩为差为三的两项,才能用裂项消去,即,
\[ \begin{aligned} {1\over(3n-2)^2}&<{1\over(3n-2-a)(3n-2+b)}\\ &={1\over a+b}\left({1\over 3n-2-a}-{1\over 3n-2+b}\right) \end{aligned} \]
对于 \(a+b=3,a\ge b\) ,最自然的想法,直接取 \(a=b=1.5\) ,
\[ \begin{aligned} 3S_n&<3+{1\over 2.5}-{1\over 5.5}+{1\over 5.5}-{1\over 8.8}+\dots+{1\over 3n-3.5}-{1\over 3n-0.5}\\ &=3+{1\over 2.5}-{1\over 3n-0.5}<3+{1\over2.5}={34\over10} \end{aligned} \]
于是,
\[ S_n<{34\over30}<{7\over6} \]
类似的,我们取 \(a=2,b=1\) 等也可以,
\[ \begin{aligned} 3S_n&<3+{1\over 2}-{1\over 4}+{1\over 4}-{1\over 7}+{1\over 7}-{1\over 10}+\dots+{1\over 3n-3}-{1\over 3n}\\ &={7\over2}-{1\over3n}<{7\over2}\\ S_n&<{7\over6} \end{aligned} \]
注意到这么做得出来的更加不准确,我们通过暴力手段可以发现,
\[ \lim_{x\to\infty}S_n\to L \]
其中 \(L\) 大约是 \(1.1217\) ,我们上面一个估算已经非常准确了。
还是例题 已知数列 \(\{a_n\}\) 是公差不为零的等差数列,
且 \(a_4\) 是 \(a_2,a_8\) 等比中项,满足,
\[ a_1+a_2+\dots+a_7=14 \]
我们注意到,
\[ a_4^2=a_2a_8 \]
而,
\[ 4^2=2\times8 \]
因此,我们大胆假设,
\[ a_n=na_1 \]
证明:
\[ a_2=a_1+d,a_4=a_1+3d,a_8=a_1+7d\\ (a_1+3d)^2=(a_1+d)(a_1+7d)\\ 6da_1+9d^2=7d^2+8da_1\\ 2d^2=2da_1,d=a_1\\ a_n=a_1+(n-1)d=na_1 \]
于是,
\[ S_7=7{a_1+a_7\over2}=28a_1=14\\ a_1={1\over2} \]
因此,
\[ a_n={1\over2}n \]
还是例题 (也许这道题是上一道题的后续
有数列 \(\{b_n\}\) 满足,
\[ b_1=-1\\ b_n={n+1\over2^{n-1}n(n-1)},n\ge2 \]
观察到 \(n(n+1)\) 的形式,裂项,
\[ \begin{aligned} b_n&={n+1\over2^{n-1}}\left({1\over n-1}-{1\over n}\right)\\ &={1\over2^{n-1}}\left({n+1\over n-1}-{n+1\over n}\right)\\ &={1\over2^{n-1}}\left({2\over n-1}-{1\over n}\right)\\ &={1\over2^{n-2}(n-1)}-{1\over 2^{n-1}n} \end{aligned} \]
考虑求和,
\[ \begin{aligned} T_n&=b_1+b_2+b_3+\dots+b_n\\ &=-1+{1\over1}-{1\over4}+{1\over4}-{1\over12}+\dots+{1\over2^{n-2}(n-1)}-{1\over 2^{n-1}n}\\ &=-{1\over2^{n-1}n} \end{aligned} \]
注意到 \(T_1=-1\) 也成立,因此上式即为结果。
又是例题 已知数列 \(\{a_n\}\) 是公差为 \(d\neq0\) 的等差数列,
且 \(\{a_{k_n}\}\) 是等比数列,其中 \(k_1=3,k_2=5,k_3=9\) 。
求 \(k_1+k_2+\dots+k_n\) 的值。 和上一题类似,我们注意到,
\[ k_1-1=2,k_2-1=4,k_3-1=8,2\times4=5 \]
我们大胆猜测,
\[ a_n=(n-1)d \]
证明,
\[ a_5^2=a_3a_9\\ (a_1+4d)^2=(a_1+2d)(a_1+8d)\\ 16d^2+8a_1d=16d^2+10a_1d\\ 4a_1d=5a_1d\\ \because d\neq0,\therefore a_1=0 \]
因此,
\[ a_n=a_1+(n-1)d=(n-1)d \]
观察 \(k_n\) 的值,
我们发现 \(3,5,9\) 是经典的数列,考虑大胆猜测(雾
\[ k_n=2^n+1 \]
此时,
\[ a_{k_n}=2^nd \]
是一个公比为 \(2\) 的等比数列,符合条件。
于是,
\[ S_n=\sum_{i=1}^nk_i=n+\sum_{i=1}^n2^i=n+2^{n+1}-2 \]
又是例题 对于数列 \(\{b_n\}\) ,有,
\[ b_n={n\over n+1}+\sqrt{n-1\over n+1} \]
求证,对于 \(n\in\mathbb N^*\) ,
\[ S_n=\sum_{i=1}^n{1\over n(n+1)\sqrt{2b_n}}<\sqrt{n\over n+1} \]
首先,我们注意到,
\[ S_1={1\over2}<\sqrt{1\over2} \]
而后面的每一步,本质是在叠加
\[ {1\over n(n+1)\sqrt{2b_n}} \]
的贡献,因此原问题的充分必要条件为,
\[ {1\over n(n+1)\sqrt{2b_n}}<\sqrt{n\over n+1}-\sqrt{n-1\over n} \]
考虑恒等变形,
\[ {1\over n(n+1)}\cdot{1\over\sqrt{2b_n}}<{n-\sqrt{n^2-1}\over\sqrt{n(n+1)}}\\ {1\over\sqrt{n(n+1)}}\cdot{1\over\sqrt{2b_n}}<n-\sqrt{n^2-1}\\ \]
注意到两边都是正数,因此,
\[ {1\over2n(n+1)b_n}<(n-\sqrt{n^2-1})^2\\ 2n(n+1)b_n>\left({1\over n-\sqrt{n^2-1}}\right)^2 \]
暂时不展开,带入,
\[ 2n^2+{\color{darkred}2n\sqrt{n^2-1}}>(n+\sqrt{n^2-1})^2=2n^2-1+{\color{darkred}2n\sqrt{n^2-1}}\\ \]
显然成立。
找规律题 已知,
\[ a_n=\prod_{2\le i\le n}{i^3-1\over i^3+1} \]
求 \(\lim_{n\to\infty}a_n\) 。 我们知道,
\[ \boxed{n^3-1=(n-1)(n^2+n+1)}\\[0.5em] \boxed{n^3+1=(n+1)(n^2-n+1)} \]
于是,首先,
\[ a_n=\prod_{2\le i\le n}{i^3-1\over i^3+1}=\prod_{2\le i\le n}{i-1\over i+1}\prod_{2\le i\le n}{i^2+i+1\over i^2-i+1} \]
左边一个乘式,
\[ \prod_{2\le i\le n}{i-1\over i+1}={1\times2\times3\times\dots\times(n-1)\over 3\times4\times\dots\times n\times(n+1)}={2\over n^2+n} \]
右边考,注意到,
\[ \boxed{(i+1)^2-(i+1)+1=i^2+i+1} \]
于是,
\[ \prod_{2\le i\le n}{i^2+i+1\over i^2-i+1}={7\times13\times\dots\times(n^2+n+1)\over3\times7\times13\times\dots}={n^2+n+1\over3} \]
得到结果,
\[ a_n={2\over3}\cdot{n^2+n+1\over n^2+n} \]
考虑极限,
\[ \lim_{n\to\infty}a_n={2\over3}\lim_{n\to\infty}{n^2+n+1\over n^2+n}={2\over3} \]
总结:找不着规律,多写几项。
总结一下 我们常见的裂项技巧有:
【简单型】一眼。
【从项出发】考虑每一项如何裂项,去消掉多余的项。
【从求和出发】考虑类似数学归纳法,证明
\[ b_n<S_n-S_{n-1}\Rightarrow b_1+b_2+\dots+b_n<S_n\;(S_0=0) \]
结论题 求,
\[ \lim_{n\to\infty}\sum_{k=1}^n\arctan{2\over k^2} \]
结论,令,
\[ \theta_1=\arctan(k+1)\\ \theta_2=\arctan(k-1) \]
则,
\[ \tan(\theta_1-\theta_2)={(k+1)-(k-1)\over 1+(k-1)(k+1)}={2\over k^2} \]
即,
\[ \arctan{2\over k^2}=\arctan(k+1)-\arctan(k-1) \]
于是,
\[ \begin{aligned} \sum_{k=1}^n\arctan{2\over k^2}&=\sum_{k=1}^n\arctan(k+1)-\sum_{k=1}^n\arctan(k-1)\\ &=\sum_{1\le k-1\le n}\arctan k-\sum_{1\le k+1\le n}\arctan k\\ &=\sum_{2\le k\le n+1}\arctan k-\sum_{0\le k\le n-1}\arctan k\\ &=\arctan(n+1)+\arctan n-\arctan0-\arctan1 \end{aligned} \]
我们知道 \(\arctan\) 的值域是 \((-\pi/2,\pi/2)\) ,因此,
\[ \lim_{k\to\infty}\arctan k=\pi/2 \]
因此,原式,
\[ \lim_{n\to\infty}\sum_{k=1}^n\arctan{2\over k^2}=\pi-{\pi\over4}={3\pi\over4} \]
回归基础 前面省略,后面,
\[ a_1=a_2=a_3=1\\ a_{n+1}={2019+a_na_{n-1}\over a_{n-2}},n>3 \]
首先正数,(显然,数列里面没有存在减法和负数,
考虑数学归纳法,对于 \(n=1,2,3\) ,有 \(a_n>0\) ,
假设对于 \(n<k(k>3)\) ,\(a_n>0\) ,考虑证明 \(a_k>0\) 。
\[ a_k={2019+a_{k-1}a_{k-2}\over a_{k-3}}>0 \]
成立,因此对于 \(n\in\mathbb N^*\) ,\(a_n>0\) 。
然后整数,我们发现 \(2019\) 是我们不想要的,怎么办捏 QAQ
我们考虑用类似特征根消掉常数的方法,错位相减,
\[ a_{k+1}a_{k-2}=2019+a_ka_{k-1}\\ a_ka_{k-3}=2019+a_{k-1}a_{k-2} \]
上减下,
\[ a_{k+1}a_{k-2}-a_ka_{k-3}=a_ka_{k-1}-a_{k-1}a_{k-2} \]
先不要冲动提右面的公因式,因为左边没有公因式 OvO
\[ a_{k-2}(a_{k+1}+a_{k-1})=a_k(a_{k-1}+a_{k-3}) \]
注意到两个括号内很现实,我们喜欢哦(
\[ \begin{aligned} {a_{k+1}+a_{k-1}\over a_k}&={a_{k-1}+a_{k-3}\over a_{k-2}}\\ b_k&=b_{k-2}(k>3) \end{aligned} \]
因此,我们有,
\[ a_1=a_2=a_3=1,a_4=2020 \]
于是,
\[ b_2={2,b_3=2021}\\ \dots\\ b_n=\left\{\begin{aligned} 2&\quad,n\equiv0\pmod2\\ 2021&\quad,n\equiv1\pmod2 \end{aligned}\right. \]
也就是,
\[ a_{k+1}=b_ka_k-a_{k-1},(k>3) \]
故都是整数。
总结:不好看的数字,没有特殊性质,考虑变形消掉。
例题 例题一 已知数列 \(\{a_n\}_{n\in\mathbb N^*}\) 满足,
\[ \forall k\in\mathbb N^*,a_{k+1}+a_k=4k+3 \]
方法一,注意到,
\[ a_{k+1}=-a_k+4k+3\\ a_k=-a_{k-1}+4k-1 \]
每个叠加的项最终只会存在变号,因此,
\[ a_k=(-1)^{k-1}a_1+\sum_{i=2}^k(-1)^{k-i}(4i-1) \]
因此,
\[ a_1+a_{2020}=\sum_{i=2}^{2020}(-1)^i(4i-1) \]
考虑扰动法,
\[ \begin{aligned} \sum_{i=2}^{2020}(-1)^i(4i-1)-(4\times2021-1)&=4\times2-1+\sum_{i=2}^{2020}(-1)^{i+1}[4(i+1)-1]\\ \sum_{i=2}^{2020}(-1)^i(4i-1)-8083&=7+\sum_{i=2}^{2020}(-1)^{i+1}(4i+3)\\ &=7-\sum_{i=2}^{2020}(-1)^i(4i-1+4)\\ &=7-\sum_{i=2}^{2020}(-1)^i(4i-1)-\sum_{i=2}^{2020}(-1)^i4\\ &=7-\sum_{i=2}^{2020}(-1)^i(4i-1)-4 \end{aligned} \]
于是,
\[ \begin{aligned} 2\sum_{i=2}^{2020}(-1)^i(4i+3)&=8086\\ \sum_{i=2}^{2020}(-1)^i(4i+3)&=4043 \end{aligned} \]
后面略,因为真的不好算。
方法二,注意到,
\[ S_{2020}={2020\over2}(a_1+a_{2020}) \]
而,
\[ \begin{aligned} S_{2020}&=(a_1+a_2)+\dots+(a_{2019}+a_{2020})\\ &=1010\times3+4\times(1+3+\dots+2019)\\ &=1010\times3+2020^2 \end{aligned} \]
则,
\[ a_1+a_{2020}={2S_{2020}\over2020}=3+4040=4043 \]
例题二:人类智慧 已知数列 \(\{a_n\}_{n\in\mathbb N^*}\) 满足,
\[ a_1=1,a_2=9\\ a_{n+2}=4a_{n+1}-3a_n-20,(n\ge1) \]
求其前 \(n\) 项和 \(S_n\) 的最大值。 注意到,减二十是很大的操作,我们充分发挥人类智慧,
于是,我们猜测数列迭代到一定程度,就会是严格单调递减的。
\[ a_1=1\\ a_2=9\\ a_3=13\\ a_4=5\\ a_5=-39\\ a_6=-191 \]
这个趋势已经很明显了,考虑证明,假设单减成立,
\[ a_{n+2}=4a_{n+1}-3a_n-20<a_{n+1}\\ 3(a_{n+1}-a_n)<20 \]
注意到当 \(n\ge3\) 时,上条件成立,那么,
\[ \begin{aligned} 3(a_{n+1}-a_n)<20&\Rightarrow a_{n+2}<a_{n+1}\\ &\Rightarrow a_{n+2}-a_{n+1}<0\\ &\Rightarrow3(a_{n+2}-a_{n+1})<20\\ &\Rightarrow a_{n+3}<a_{n+2}\\ &\Rightarrow\dots \end{aligned} \]
即,对于 \(n\ge3\) ,
\[ a_{n+1}<a_n \]
于是,观察我们的列表,可以得出,
\[ a_n<0,(n\ge5) \]
于是,
\[ S_{n\max}=S_n|_{n=4}=1+9+13+5=28 \]
当然也可以求出通项公式,
\[ a_n=10n-2\times3^{n-1}-8 \]
当 \(n\) 很大时,幂远大于线性,因此数列越来越小。
例题三:邻项相减 一些记号省略了,后面,
\[ S_n=(-1)^na_n+{1\over2^n}+n-3 \]
邻项相减(或者说前缀和的差分),
\[ S_n=(-1)^na_n+{1\over2^n}+n-3\\ S_{n-1}=-(-1)^na_{n-1}+2\cdot{1\over2^n}+n-4 \]
相减,
\[ a_n=S_n-S_{n-1}=(-1)^na_n+(-1)^na_{n-1}-{1\over2^n}+1 \]
分讨奇偶性,
\[ a_{2k}=a_{2k}+a_{2k-1}-{1\over2^{2k}}+1\\ a_{2k-1}=-a_{2k-1}-a_{2k-2}-{1\over2^{2k-1}}+1 \]
整理上面的,得,
\[ a_{2k-1}={1\over2^{2k}}-1 \]
对于下面的,
\[ \begin{aligned} a_{2k-2}&=-2a_{2k-1}-{1\over2^{2k-1}}+1\\ &=-{1\over2^{2k-1}}+2-{1\over2^{2k-1}}+1\\ &=-{1\over2^{2k-2}}+3\\ a_{2k}&=-{1\over2^{2k}}+3 \end{aligned} \]
于是,
\[ a_n=\left\{\begin{aligned} {1\over2^{n+1}}-1&\quad\text{if $n$ 是奇数}\\ -{1\over2^n}+3&\quad\text{if $n$ 是偶数}\\ \end{aligned}\right. \]
简单题 数列 \(\{a_n\}\) 满足,
\[ a_1=3, a_{n+1}=a_n^2-3a_n+4 \]
A. \(\{a_n\}\) 严格单调递增。\(\{a_n\}\) 无界。\(a_{100}=101\) .\(\displaystyle\lim_{n\to\infty}\left({1\over a_1-1}+{1\over a_2-1}+\dots+{1\over a_n-1}\right)=1\) .
容易发现,右侧系数 \(134\) 类似 \(144\) 的完全平方式,
\[ a_{n+1}-a_n=a_n^2-4a_n+4=(a_n-2)^2\ge0\\ a_{n+1}\ge a_n,\therefore a_n\ge\dots\ge a_1=3\\ (a_n-2)^2\ge1\Rightarrow a_{n+1}>a_n \]
由上面的,
\[ a_{n+1}-a_n=(a_n-2)^2\ge1\\ a_n\ge a_{n+1}\\ a_2\ge4,a_3\ge5,\dots,a_n\ge n+2 \]
于是,数列无界且,
\[ a_{100}\ge102 \]
后面不会了,注意到迭代形如 \(a_{n+1}=f(a_n)\) ,我们知道不动点是一个好工具,
\[ x=f(x)\\ x=x^2-3x+4\\ x^2-4x+4=0\\ (x-2)^2=0\\ x=2 \]
递归式两边同时减二,取倒数,
\[ a_{n+1}-2=a_n^2-3a_n+2=(a_n-1)(a_n-2)\\ {1\over a_{n+1}-2}={1\over(a_n-1)(a_n-2)}={1\over a_n-2}-{1\over a_n-1}\\ {1\over a_n-1}={1\over a_n-2}-{1\over a_{n+1}-2} \]
注意到形如 \(f(n)=g(n)-g(n')\) 的形式,裂项成功,
\[ {1\over a_1-1}+{1\over a_2-1}+\dots+{1\over a_n-1}\\ ={1\over a_1-2}-{1\over a_2-2}+{1\over a_2-2}-{1\over a_3-2}+\dots+{1\over a_n-2}-{1\over a_{n+1}-2}\\ ={1\over a_1-2}-{1\over a_{n+1}-2}=1-{1\over a_{n+1}-2} \]
注意到,
\[ 0<{1\over a_{n+1}-2}\le{1\over n+1} \]
因此这一项极限为 \(0\) ,
\[ \lim_{n\to\infty}\left({1\over a_1-1}+{1\over a_2-1}+\dots+{1\over a_n-1}\right)=1 \]
成立,故选 ABD。
签到题 数列,
\[ a_1=1, a_{n+1}=\sqrt{a_n^2+{1\over a_n^{2019}}} \]
判断数列 \(\{a_n\}\) 是否有界。
注意到该数列每一项均为正数,且都非零,
\[ a_{n+1}^2=a_n^2+{1\over a_n^{2019}}\\ a_{n+1}^2> a_n^2\\ a_{n+1}> a_n \]
严格单调递增,故无界。
证明,反证法:
假设数列有界,记为 \(L\) ,两边取极限,
\[ L^2=L^2+{1\over L^{2019}} \]
显然无界,不成立。
数学归纳法 数学归纳法是证明某个命题对于所有满足 \(n\ge n_0\) 的整数 \(n\) 都成立的一般方法。首先我们在 \(n\) 取 最小值 \(n_0\) 时证明该命题,这一步骤成为基础 。然后对 \(n>n_0\) ,假设该命题对 \(n_0\sim n-1\) 之间的所有值已经被证明,再证明该命题对 \(n\) 成立,这一步骤成为归纳 。
这样一种证明方法仅用有限步就得到无限多个结果。
皮亚诺公理 一个最简单的例子,皮亚诺公理的自然数定义:
\(0\) 是自然数;每一个确定的自然数 \(a\) ,都有一个确定的后继 \(a'\) ,\(a'\) 也是自然数; 对于每个自然数 \(b,c\) ,\(b=c\) 当且仅当 \(b'=c'\) ; \(0\) 不是任何自然数的后继;任意关于自然数的命题,如果证明: 它对 \(0\) 成立,且假定它对自然数 \(a'\) 为真时, 可以证明它对 \(a'\) 也成立。 那么该命题对所有自然数都成立。 公理 \(5\) 保证了数学归纳法的正确性,从而被称为归纳法原理。
PS:在集合论和计算机科学领域中,认为 \(0\) 属于自然数。
但在数论领域中,认为 \(0\) 不属于自然数,因而按数论描述,自然数会同义于正整数。
因此,如果定义 \(0\) 不属于自然数,把上面的 \(0\) 改成 \(1\) 即可。
戴德金-皮亚诺结构 戴德金-皮亚诺结构可以描述为满足所有以下条件的三元组 \((S,f,e)\) :
\((e\in S)\) \((\forall a\in S)(f(a)\in S)\) \((\forall b\in S)(\forall c\in S)((f(b)=f(c))\Rightarrow(b=c))\) \((\forall a\in S)(f(a)\neq e)\) \((\forall A\subseteq S)(((e\in A)\wedge(\forall a\in A)(f(a)\in A))\Rightarrow(A=S))\) 一个形象化的例子就是最上面的,即三元组 \((\mathbb N,(f:\mathbb N\to\mathbb N_+;\;x\mapsto(x+1)),0)\) 。
例子 证明,
\[ S_n=1+2+\dots+n={n(n+1)\over2} \]
由于,
\[ 1={1\times2\over2} \]
假设我们已经证明,
\[ S_{n-1}={n(n-1)\over2} \]
那么,
\[ S_n=S_{n-1}+n={n(n-1)\over2}+n={n(n+1)\over2} \]
则,其对于任意自然数成立。
应用 解递归式,
\[ Q_0=\alpha,Q_1=\beta\\ Q_n={1+Q_{n-1}\over Q_{n-2}},n>1 \]
容易发现,
\[ \begin{array}{c|c} \begin{aligned} Q_0&=\alpha\\ Q_1&=\beta\\ Q_2&={1+\beta\over\alpha}\\ Q_3&={1+\alpha+\beta\over\alpha\beta}\\ Q_4&={1+\alpha\over\beta} \end{aligned}& \begin{aligned} Q_5&=\alpha\\ Q_6&=\beta\\ \dots\\\\\\\\\\ \end{aligned} \end{array} \]
是一个周期函数,结论:
\[ Q_n=\left\{\begin{aligned} &\alpha&\kern{1em}\operatorname{if}n\equiv0\pmod5\\ &\beta&\kern{1em}\operatorname{if}n\equiv1\pmod5\\ &{1+\beta\over\alpha}&\kern{1em}\operatorname{if}n\equiv2\pmod5\\ &{1+\alpha+\beta\over\alpha\beta}&\kern{1em}\operatorname{if}n\equiv3\pmod5\\ &{1+\alpha\over\beta}&\kern{1em}\operatorname{if}n\equiv4\pmod5\\ \end{aligned}\right. \]
证明:
对于 \(n\in[0,5)\) ,易证。
假设对于 \(n=5k+q,k\le t,k\in\mathbb Z,q\in[0,5)\) 成立。
证明对于 \(n=5(k+1)+q\) 也成立,以 \(n=5(k+1)\) 为例,
\[ Q_{5(k+1)}={1+Q_{5(k+1)-1}\over Q_{5(k+1)-2}}={1+Q_{5k+4}\over Q_{5k+3}}=\alpha \]
对于 \(q=2,3,4\) ,同理,略。
反向数学归纳法 反向数学归纳法,是从 \(n\) 到 \(n-1\) 来证明命题,而不是相反。
例如,证明:
\[ \prod_{i=1}^nx_i\le\left({\sum_{i=1}^nx_i\over n}\right)^n \]
对于 \(x_1,x_2\dots x_n\ge0\) 。
证明:
记命题,
\[ P(n):x_1\dots x_n\le\left({x_1+\dots+x_n\over n}\right)^n \]
则,
\[ P(1):x_1\le x_1 \]
显然成立。
\[ P(2):x_1x_2\le\left({x_1+x_2\over2}\right)^2 \]
即,
\[ 4x_1x_2\le x_1^2+2x_1x_2+x_2^2\\ x_1^2-2x_1x_2+x_2^2\ge0 \]
显然成立。
即,\(P(1),P(2)\) 成立。
性质一 若 \(P(n)\) 成立,则 \(P(n-1)\) 也成立。
记,
\[ x_n={x_1+\dots+x_{n-1}\over n-1} \]
则 \(P(n)\) 为,
\[ x_1\dots x_{n-1}\cdot{x_1+\dots+x_{n-1}\over n-1}\le\left({x_1+\dots+x_{n-1}\over n-1}\right)^n \]
即 \(P(n-1)\) ,
\[ x_1\dots x_{n-1}\le\left({x_1+\dots+x_{n-1}\over n-1}\right)^{n-1} \]
Q.E.D.
性质二 若 \(P(n)\) 成立,则 \(P(2n)\) 成立。
我们记第一个 \(P(n)\) 为,
\[ x_1\dots x_n\le\left({x_1+\dots+x_n\over n}\right)^n \]
同样的,记第二个 \(P(n)\) 为,
\[ x_{n+1}\dots x_{2n}\le\left({x_{n+1}+\dots+x_{2n}\over n}\right)^n \]
我们知道 \(P(2)\) 是成立的,记
\[ y_1=x_1\dots x_n\\ y_2=x_{n+1}\dots x_{2n} \]
对 \(y_1,y_2\) 应用 \(P(2)\) ,
\[ \begin{aligned} y_1y_2&\le\left({y_1+y_2\over2}\right)^2\\ x_1\dots x_{2n}&\le\left(x_1\dots x_n+x_{n+1}\dots x_{2n}\over2\right)^2\\ &={(x_1\dots x_n)^2+(x_{n+1}+x_{2n})^2+2x_1\dots x_{2n}\over4}\\ &={(x_1\dots x_n)^2+(x_{n+1}+x_{2n})^2\over2}\\ &\le{(x_1+\dots+x_n)^{2n}+(x_{n+1}+\dots+x_{2n})^{2n}\over(2n)^{2n}}\\ &\le\left({x_1+\dots+x_{2n}\over2n}\right)^{2n} \end{aligned} \]
即,\(P(2n)\) 。
Q.E.D.
整理 根据,
\[ P(1),P(2)\\ P(n)\Rightarrow P(2n)\\ P(n)\Rightarrow P(n-1) \]
我们可以知道,对于 \(\forall n\in\mathbb N^*\) ,\(P(n)\) 成立。
END.
正在加载中 ,更新历史 。在 GitHub 上编辑此页 !RainPPR 。