树上莫队¶

简述¶

分为，

查询链信息；
查询子树信息。

如果是查询子树信息的理想莫队信息，

那么可以启发式合并，是 polylog 的（例如普通莫队例题四）。

下面直接讨论查询链信息。

括号序分块¶

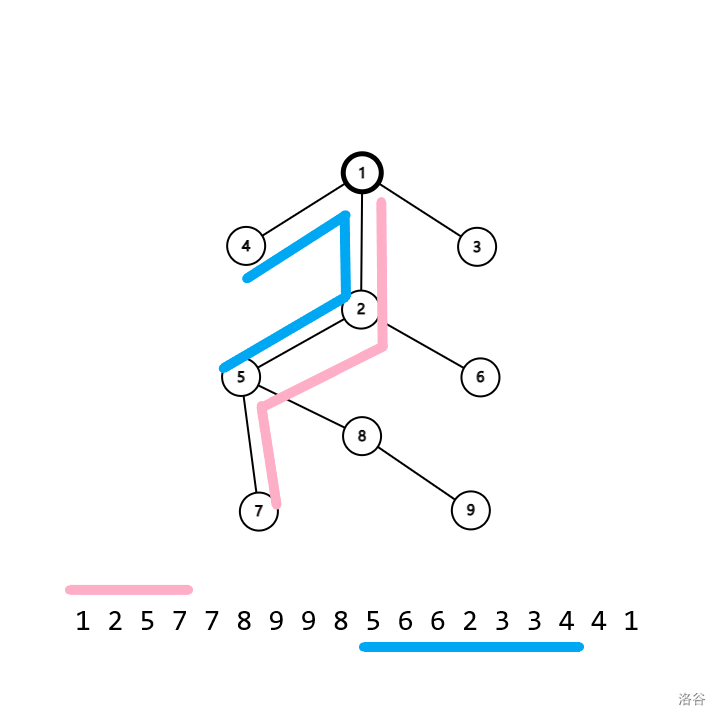
一般的莫队只能处理线性问题，我们要把树强行压成序列。

我们可以将树的括号序跑下来，把括号序分块，在括号序上跑莫队。

我们 DFS 树的时候，

进入 \(x\) 点就 \(\text{push}(+x)\)；
走出 \(x\) 点就 \(\text{push}(-x)\)。

然后在挪动指针（莫队转移）的时候，

如果新加入的值是 \(+x\)，就加入 \(x\)，add(x)；
如果新加入的值是 \(-x\)，就删除 \(x\)，del(x)。
如果新删除的值是 \(+x\)，就删除 \(x\)，del(x)；
如果新删除的值是 \(-x\)，就加入 \(x\)，add(x)。

可以理解为，从根开始的路径，下去为正，上去为负，

那么，一个多余子树的内容，就被抵消了（代码上容易被处理）。

实现上，与我们上面的理论有很多不同的地方。

实现¶

点权 / 边权¶

我们通常对点权离散化，

int n, m, c[N];
cin >> n >> m;
vector<int> s(n);
for (int i = 1; i <= n; ++i) {
    cin >> c[i];
    s[i - 1] = c[i];
}
sort(s.begin(), s.end());
s.erase(unique(s.begin(), s.end()), s.end());
for (int i = 1; i <= n; ++i)
    c[i] = lower_bound(s.begin(), s.end(), c[i]) - s.begin() + 1;

对于边权，通常下放到点权。

路径的转化¶

对于点权，

我们发现，

对于一条直的路径 \((u,v)\)，在括号序上面表示为 \(s(u)\sim s(v)\)
而一条拐弯的路径表示为，\(e(u)\sim s(v)\)，加上消失的 \(\text{LCA}\)。

假设 \(s(u)<s(v)\)。

于是，我们重链剖分求一下 LCA 顺便预处理括号序即可。

实现

vector<int> g[N];

int fa[N], son[N];
int dep[N], siz[N];

int tot, top[N];
int dfs[2 * N], st[N], ed[N];

void dfs1(int u, int ff) {
    dfs[++tot] = u, st[u] = tot;
    int mx = -1;
    siz[u] = 1, son[u] = -1;
    for (int v : g[u]) {
        if (v == ff) continue;
        fa[v] = u, dep[v] = dep[u] + 1;
        dfs1(v, u), siz[u] += siz[v];
        if (siz[v] > mx) mx = siz[v], son[u] = v;
    }
    dfs[++tot] = u, ed[u] = tot;
}

void dfs2(int u, int _top) {
    top[u] = _top;
    if (son[u] == -1) return;
    dfs2(son[u], _top);
    for (int v : g[u]) {
        if (v == fa[u]) continue;
        if (v == son[u]) continue;
        dfs2(v, v);
    }
}

int lca(int u, int v) {
    while (top[u] != top[v]) {
        if (dep[top[u]] > dep[top[v]])
            u = fa[top[u]];
        else
            v = fa[top[v]];
    }
    return dep[u] < dep[v] ? u : v;
}

// Main

for (int i = 1; i < n; ++i) {
    int u, v;
    cin >> u >> v;
    g[u].push_back(v);
    g[v].push_back(u);
}

dfs1(1, -1), dfs2(1, 1);

for (int i = 1; i <= m; ++i) {
    int x, y; cin >> x >> y;
    if (st[x] > st[y]) swap(x, y);
    int l = lca(x, y);
    if (l == x) q[i] = {i, st[x], st[y], -1};
    else q[i] = {i, ed[x], st[y], l};
}

对于边权，我们发现下放之后要反过来，

if (st[x] > st[y]) swap(x, y);
int l = lca(x, y);
if (l == x) q[i] = {i, st[x], st[y], l};
else q[i] = {i, ed[x], st[y], -1};

这很好理解。

莫队算法部分¶

我们发现，

若一个点是第一次被计算，那么一定是加入，否则一定是删除。

据此，我们可以不用管上面奇奇怪怪的理论部分，

实现

int block, belong[2 * N];

struct query {
    int id, l, r, lca;
    friend bool operator <(const query &a, const query &b) {
        if (belong[a.l] != belong[b.l]) return a.l < b.l;
        return belong[a.l] & 1 ? a.r < b.r : a.r > b.r;
    }
} q[M];

void add(int x) {
    x = c[x];
    // do something ...
}

void del(int x) {
    x = c[x];
    // do something ...
}

int get_ans() {
    // do something ...
}

void calc(int x) {
    vis[x] ? del(x) : add(x);
    vis[x] ^= 1;
}

int ans[M];

// Main

block = max(1, int(tot / sqrt(m * 2 / 3.0)));
for (int i = 1; i <= tot; ++i) belong[i] = (i - 1) / block + 1;

sort(q + 1, q + m + 1);

int l = 1, r = 0;
for (int i = 1; i <= m; ++i) {
    int x = q[i].l, y = q[i].r;
    while (x < l) calc(dfs[--l]);
    while (y > r) calc(dfs[++r]);
    while (x > l) calc(dfs[l++]);
    while (y < r) calc(dfs[r--]);
    if (q[i].lca != -1) calc(q[i].lca);
    ans[q[i].id] = get_ans();
    if (q[i].lca != -1) calc(q[i].lca);
}

for (int i = 1; i <= m; ++i) cout << ans[i] << endl;

例题¶

例题一：SP10707 COT2 - Count on a tree II¶

求树上两节点简单路径中的点的不同颜色数。

经典例题，就是上面的代码。

点击查看代码

#include <bits/stdc++.h>

using namespace std;

#define endl "\n"

constexpr int N = 4e4 + 10;
constexpr int M = 1e5 + 10;

int n, m, c[N];

int block, belong[2 * N];

vector<int> g[N];

struct query {
    int id, l, r, lca;
    friend bool operator <(const query &a, const query &b) {
        if (belong[a.l] != belong[b.l]) return a.l < b.l;
        return belong[a.l] & 1 ? a.r < b.r : a.r > b.r;
    }
} q[M];

// -----------------------------------------------------------------------------

int fa[N], son[N];
int dep[N], siz[N];

int tot, top[N];
int dfs[2 * N], st[N], ed[N];

void dfs1(int u, int ff) {
    dfs[++tot] = u, st[u] = tot;
    int mx = -1;
    siz[u] = 1, son[u] = -1;
    for (int v : g[u]) {
        if (v == ff) continue;
        fa[v] = u, dep[v] = dep[u] + 1;
        dfs1(v, u), siz[u] += siz[v];
        if (siz[v] > mx) mx = siz[v], son[u] = v;
    }
    dfs[++tot] = u, ed[u] = tot;
}

void dfs2(int u, int _top) {
    top[u] = _top;
    if (son[u] == -1) return;
    dfs2(son[u], _top);
    for (int v : g[u]) {
        if (v == fa[u]) continue;
        if (v == son[u]) continue;
        dfs2(v, v);
    }
}

int lca(int u, int v) {
    while (top[u] != top[v]) {
        if (dep[top[u]] > dep[top[v]])
            u = fa[top[u]];
        else
            v = fa[top[v]];
    }
    return dep[u] < dep[v] ? u : v;
}

// -----------------------------------------------------------------------------

bool vis[2 * N];

int res, bucket[N];

void add(int x) {
    x = c[x];
    if (++bucket[x] == 1) ++res;
}

void del(int x) {
    x = c[x];
    if (--bucket[x] == 0) --res;
}

void calc(int x) {
    vis[x] ? del(x) : add(x);
    vis[x] ^= 1;
}

int ans[M];

int get_ans() {
    return res;
}

// -----------------------------------------------------------------------------

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> n >> m;
    vector<int> s(n);
    for (int i = 1; i <= n; ++i)
        cin >> c[i], s[i - 1] = c[i];
    sort(s.begin(), s.end());
    s.erase(unique(s.begin(), s.end()), s.end());
    for (int i = 1; i <= n; ++i)
        c[i] = lower_bound(s.begin(), s.end(), c[i]) - s.begin() + 1;
    for (int i = 1; i < n; ++i) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs1(1, -1), dfs2(1, 1);
    for (int i = 1; i <= m; ++i) {
        int x, y; cin >> x >> y;
        if (st[x] > st[y]) swap(x, y);
        int l = lca(x, y);
        if (l == x) q[i] = {i, st[x], st[y], -1};
        else q[i] = {i, ed[x], st[y], l};
    }
    block = max(1, int(tot / sqrt(m * 2 / 3.0)));
    for (int i = 1; i <= tot; ++i)
        belong[i] = (i - 1) / block + 1;
    sort(q + 1, q + m + 1);
    int l = 1, r = 0;
    for (int i = 1; i <= m; ++i) {
        int x = q[i].l, y = q[i].r;
        while (x < l) calc(dfs[--l]);
        while (y > r) calc(dfs[++r]);
        while (x > l) calc(dfs[l++]);
        while (y < r) calc(dfs[r--]);
        if (q[i].lca != -1) calc(q[i].lca);
        ans[q[i].id] = get_ans();
        if (q[i].lca != -1) calc(q[i].lca);
    }
    for (int i = 1; i <= m; ++i)
        cout << ans[i] << endl;
    return 0;
}

例题二：QOJ7245 Frank Sinatra¶

求路径边权 \(\operatorname{mex}\)。

我们把点权下放，直接值域分块处理即可，类似 P4137 Rmq Problem / mex。

此处一个技巧就是，值域为 \([0,n]\) 的序列 \(\operatorname{mex}\) 一定在 \([0,n+1]\) 中，也就是更大的没有意义了。

点击查看代码

#define NDEBUG 1

#include <bits/stdc++.h>

using namespace std;

#define endl "\n"

constexpr int N = 1e5 + 10;

// -----------------------------------------------------------------------------

int n, m;

struct edge {
    int v, w;
    edge() = default;
    edge(int v, int w): v(v), w(w) {}
};

vector<edge> g[N];

int col[N];

// -----------------------------------------------------------------------------

int dfs[2 * N], tot;
int st[N], ed[N];

namespace hld {
    int fa[N], son[N];
    int dep[N], siz[N];
    int top[N];

    void dfs1(int u, int ff) {
        dfs[++tot] = u, st[u] = tot;
        siz[u] = 1, son[u] = -1;
        int mx = -1;
        for (auto t : g[u]) {
            int v = t.v;
            if (v == ff) continue;
            col[v] = t.w;
            fa[v] = u, dep[v] = dep[u] + 1;
            dfs1(v, u), siz[u] += siz[v];
            if (siz[v] > mx) mx = siz[v], son[u] = v;
        }
        dfs[++tot] = u, ed[u] = tot;
    }

    void dfs2(int u, int tp) {
        top[u] = tp;
        if (son[u] == -1) return;
        dfs2(son[u], tp);
        for (auto t : g[u]) {
            if (t.v == fa[u]) continue;
            if (t.v == son[u]) continue;
            dfs2(t.v, t.v);
        }
    }
}

int lca(int u, int v) {
    while (hld::top[u] != hld::top[v]) {
        if (hld::dep[hld::top[u]] > hld::dep[hld::top[v]])
            u = hld::fa[hld::top[u]];
        else v = hld::fa[hld::top[v]];
    }
    return hld::dep[u] < hld::dep[v] ? u : v;
}

// -----------------------------------------------------------------------------

int block1, belong1[2 * N];

struct query {
    int id, l, r, lca;
    friend bool operator <(const query &a, const query &b) {
        if (belong1[a.l] != belong1[b.l]) return a.l < b.l;
        return belong1[a.l] & 1 ? a.r < b.r : a.r > b.r;
    }
} q[N];

// -----------------------------------------------------------------------------

bool vis[2 * N];

int block, cnt;
int belong[N], L[N], R[N];
int bucket[N], appr[N];

void add(int x) {
    ++x;
    if (x > n) return;
    if (!bucket[x]) ++appr[belong[x]];
    ++bucket[x];
}

void del(int x) {
    ++x;
    if (x > n) return;
    --bucket[x];
    if (!bucket[x]) --appr[belong[x]];
}

int get_ans() {
    int inner = 1;
    while (inner <= cnt && appr[inner] == R[inner] - L[inner] + 1) ++inner;
    for (int i = L[inner]; i <= R[inner]; ++i) if (!bucket[i]) return i - 1;
    __builtin_unreachable();
    return 0;
}

void calc(int x) {
    if (vis[x]) del(col[x]);
    else add(col[x]);
    vis[x] ^= 1;
}

// -----------------------------------------------------------------------------

int ans[N];

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> n >> m;
    // ???????
    block = sqrt(n), cnt = (n - 1) / block + 1;
    for (int i = 1; i <= n; ++i) belong[i] = (i - 1) / block + 1;
    for (int i = 1; i <= cnt; ++i) R[i] = i * block, L[i] = R[i] - block + 1;
    R[cnt] = n;
    // ????
    for (int i = 2; i <= n; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        g[u].emplace_back(v, w);
        g[v].emplace_back(u, w);
    }
    // ?????
    hld::dfs1(1, -1);
    hld::dfs2(1, 1);
    col[1] = 1;
    for (int i = 1; i <= m; ++i) {
        int u, v;
        cin >> u >> v;
        if (st[u] > st[v]) swap(u, v);
        int l = lca(u, v);
        if (l == u) q[i] = query{i, st[u], st[v], l};
        else q[i] = query{i, ed[u], st[v], -1};
    }
    block1 = max(1, int(tot / sqrt(m * 2 / 3.0)));
    for (int i = 1; i <= tot; ++i) belong1[i] = (i - 1) / block1 + 1;
    sort(q + 1, q + m + 1);
    // ????
    int l = 1, r = 0;
    for (int i = 1; i <= m; ++i) {
        int x = q[i].l, y = q[i].r;
        while (x < l) calc(dfs[--l]);
        while (y > r) calc(dfs[++r]);
        while (x > l) calc(dfs[l++]);
        while (y < r) calc(dfs[r--]);
        if (q[i].lca != -1) calc(q[i].lca);
        ans[q[i].id] = get_ans();
        if (q[i].lca != -1) calc(q[i].lca);
    }
    for (int i = 1; i <= m; ++i)
        cout << ans[i] << endl;
    return 0;
}

例题三：Baekjoon13892 ACM Tax¶

同上。

点击查看代码

#ifndef M_DEBUG
#define NDEBUG 1
#define FAST_IO 1
#define D(x) ({ void(0); })
#else
#define D(x) ({ cerr << "| DEBUG #" << __LINE__ << " IN " << __FUNCTION__ << "() \t| \t" << #x << " = \t[" << (x) << "]\n"; void(0); })
#endif

#include <bits/stdc++.h>

#ifdef FAST_IO
#define endl "\n"
#endif

using namespace std;

// -----------------------------------------------------------------------------

// constexpr int N = 5e4 + 10;
constexpr int N = 1e5 + 10;
constexpr int M = 1e5 + 10;

// -----------------------------------------------------------------------------

int n, m;
int col[N];

struct edge {
    int v, w;
    edge() = default;
    edge(int v, int w): v(v), w(w) {}
};

vector<edge> g[N];

// -----------------------------------------------------------------------------

int fa[N], siz[N];
int son[N], dep[N];

int dfs[2 * N], tot;
int st[N], ed[N];

void dfs1(int u, int ff) {
    dfs[++tot] = u;
    st[u] = tot;
    son[u] = -1;
    siz[u] = 1;
    int mx = -1;
    for (auto t : g[u]) {
        int v = t.v;
        if (v == ff) continue;
        col[v] = t.w;
        fa[v] = u;
        dep[v] = dep[u] + 1;
        dfs1(v, u);
        siz[u] += siz[v];
        if (siz[v] > mx) {
            mx = siz[v];
            son[u] = v;
        }
    }
    dfs[++tot] = u, ed[u] = tot;
}

int top[N];

void dfs2(int u, int to) {
    top[u] = to;
    if (son[u] == -1) return;
    dfs2(son[u], to);
    for (auto t : g[u]) {
        int v = t.v;
        if (v == fa[u]) continue;
        if (v == son[u]) continue;
        dfs2(v, v);
    }
}

int lca(int x, int y) {
    while (top[x] != top[y]) {
        if (dep[top[x]] > dep[top[y]]) x = fa[top[x]];
        else y = fa[top[y]];
    }
    if (dep[x] > dep[y]) return y;
    return x;
}

// -----------------------------------------------------------------------------

int block, belong[2 * N];

struct query {
    int id, l, r, lca;
    friend bool operator <(const query &a, const query &b) {
        if (belong[a.l] != belong[b.l]) return a.l < b.l;
        return belong[a.l] & 1 ? a.r < b.r : a.r > b.r;
    }
} Q[M];

// -----------------------------------------------------------------------------

struct ans {
    int val;
    bool ft;
    ans(): val(0), ft(0) {}
    ans(int val): val(val), ft(0) {}
    ans(double val): val(int(val)), ft(val - int(val) != 0) {}
    friend ostream& operator <<(ostream &out, const ans &x) {
        out << x.val << (x.ft ? ".5" : ".0");
        return out;
    }
} Ans[M];

constexpr int MAXV = 1e5;
constexpr int V = MAXV + 10;

int block2, belong2[V];
int cnt2, L[V], R[V];

void init2() {
    block2 = sqrt(MAXV);
    cnt2 = (MAXV - 1) / block2 + 1;
    for (int i = 1; i <= MAXV; ++i)
        belong2[i] = (i - 1) / block2 + 1;
    for (int i = 1; i <= cnt2; ++i)
        R[i] = i * block2, L[i] = R[i] - block2 + 1;
    R[cnt2] = V;
}

int arr[V], sum[V];

void modify(int x, int v) {
    arr[x] += v;
    sum[belong2[x]] += v;
}

int rnk(int k) {
    int inner = 1;
    while (sum[inner] < k)
        k -= sum[inner], ++inner;
    for (int i = L[inner]; i <= R[inner]; ++i) {
        k -= arr[i];
        if (k <= 0) return i;
    }
    __builtin_unreachable();
}

int cnt;

void add(int x) {
    ++cnt;
    modify(x, 1);
}

void del(int x) {
    --cnt;
    modify(x, -1);
}

ans get_ans() {
    if (cnt & 1)
        return rnk((cnt + 1) >> 1);
    return (rnk((cnt >> 1) + 1) + rnk(cnt >> 1)) / 2.0;
}

int vis[2 * N];

void calc(int x) {
    if (vis[x])
        del(col[x]);
    else
        add(col[x]);
    vis[x] ^= 1;
}

// -----------------------------------------------------------------------------

void clear() {
    memset(arr, 0, sizeof arr);
    memset(sum, 0, sizeof sum);
    for (int i = 1; i <= n; ++i)
        g[i].clear(), g[i].shrink_to_fit();
    cnt = tot = dep[1] = 0;
    memset(vis, 0, sizeof(int) * n * 2);
}

void Main() {
    cin >> n;
    clear();
    for (int i = 2; i <= n; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        g[u].emplace_back(v, w);
        g[v].emplace_back(u, w);
    }
    dfs1(1, -1);
    dfs2(1, 1);
    col[1] = 1;
    cin >> m;
    for (int i = 1; i <= m; ++i) {
        int x, y;
        cin >> x >> y;
        if (st[x] > st[y]) swap(x, y);
        int l = lca(x, y);
        if (x == l) Q[i] = {i, st[x], st[y], l};
        else Q[i] = {i, ed[x], st[y], -1};
    }
    block = max(1, int(tot / sqrt(m * 2.0 / 3)));
    for (int i = 1; i <= tot; ++i)
        belong[i] = (i - 1) / block + 1;
    sort(Q + 1, Q + m + 1);
    int l = 1, r = 0;
    for (int i = 1; i <= m; ++i) {
        int x = Q[i].l, y = Q[i].r;
        if (x == y) {
            Ans[Q[i].id] = col[dfs[x]];
            continue;
        }
        while (x < l) calc(dfs[--l]);
        while (y > r) calc(dfs[++r]);
        while (x > l) calc(dfs[l++]);
        while (y < r) calc(dfs[r--]);
        if (Q[i].lca != -1) calc(Q[i].lca);
        Ans[Q[i].id] = get_ans();
        if (Q[i].lca != -1) calc(Q[i].lca);
    }
    for (int i = 1; i <= m; ++i) {
        cout << Ans[i] << endl;
    }
}

signed main() {
    #ifdef FAST_IO
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    #endif
    init2();
    int T;
    cin >> T;
    while (T--)
        Main();
    return 0;
}

本页面最近更新：正在加载中，更新历史。
编辑页面：在 GitHub 上编辑此页！
本页面贡献者：RainPPR。