树状数组基础¶
引入¶
树状数组的特点:
- 好写好调。
- 一般只支持单点修改,前缀查询。
- 可以通过差分、公式等实现区间修改,单点查询等。
我们考虑这样一个题:
- 单调修改,区间求和。
我们有两个比较好想的思路:
- 直接 \(\mathcal O(1)\) 修改,\(\mathcal O(n)\) 遍历查询;
- 维护前缀和 \(\mathcal O(1)\) 查询,\(\mathcal O(n)\) 修改贡献。
而树状数组提供了一个每个操作单次 \(\mathcal O(\log n)\) 的做法。
基本思想¶
代数上,太复杂了我们不考虑。
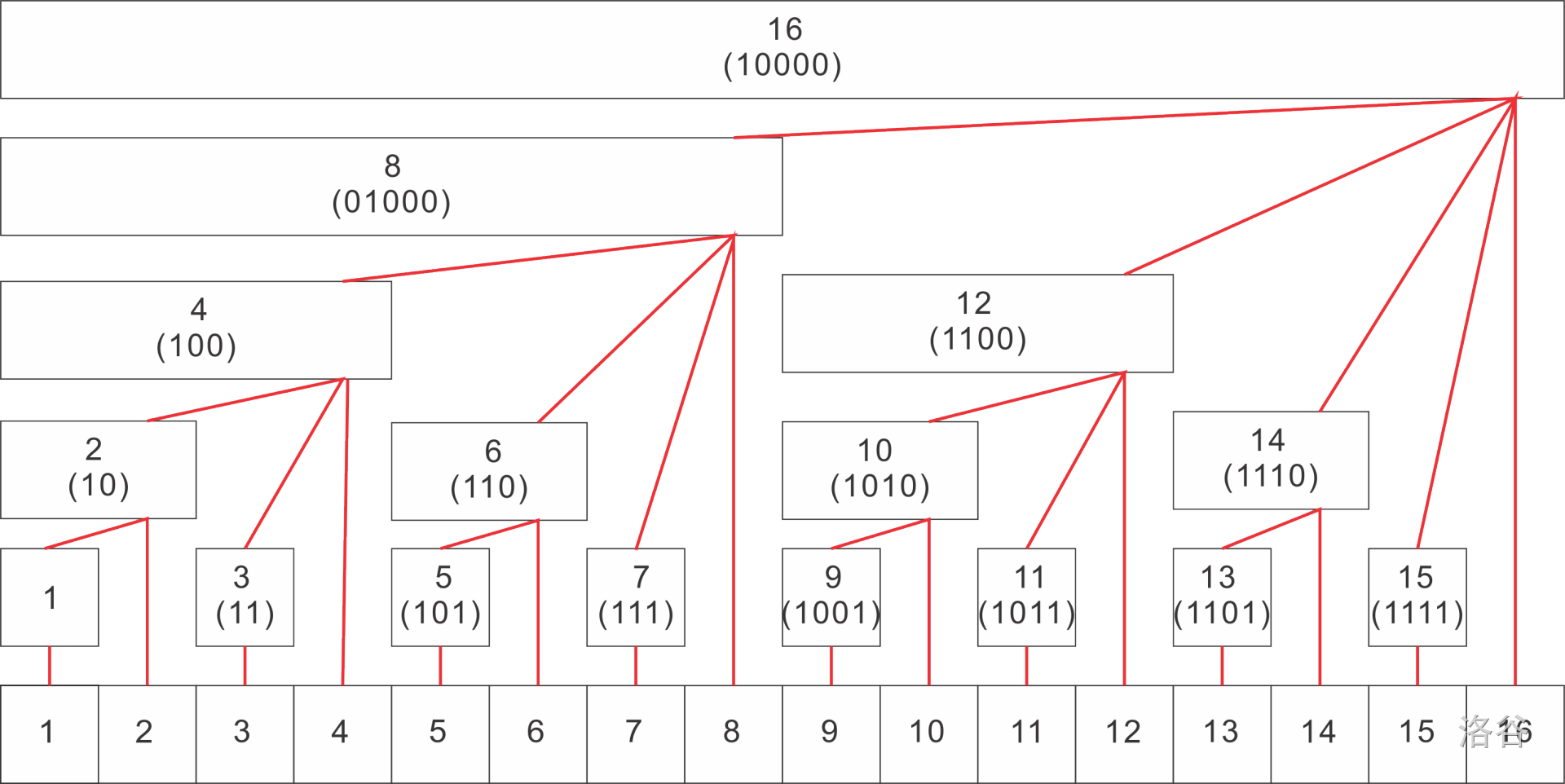
几何上,如图,
我们令 \(s_i\) 表示,
- 从 \(i\) 往前数 \(\operatorname{lowbit(i)}\) 位的和,即 \(a(i-\operatorname{lowbit}(i)+1,,i)\)。
那么我们就知道,前缀和可以表示为若干个这样的区间。
可以发现,任何一个前缀都可以被 \(\mathcal O(\log n)\) 个小块表示,因此复杂度正确。
代码实现:
constexpr int N = 1e5 + 10;
#define lowbit(x) ((x) & -(x))
int n, s[N];
// [1, x]
int query(int x) {
int r = 0;
for (; x; x -= lowbit(x)) r += s[x];
return r;
}
// [x] += v
int modify(int x, int v) {
for (; x <= n; x += lowbit(x)) s[x] += v;
}
// [l, r]
int query(int l, int r) {
if (l == 1) return query(r);
return query(r) - query(l - 1);
}请注意:
- 树状数组不支持负数及零下标,可以使用偏移量或者离散化;
- 树状数组本身只支持单点修改,前缀查询,可以通过数学方法来实现其他的。
差分实现区间修改,单点查询。
我们将原数组 \(s\) 变为其差分数组,那么,
- 区间修改,差分性质即可;
- 单点查询,注意到原数组即差分数组的前缀和,符合树状数组维护的性质。
代码实现:
int add(int p, int q, int v) {
modify(p, v);
modify(q + 1, -v);
}
int at(int x) {
return query(x);
}区间修改,区间查询。
推式子,感觉不如线段树直接维护,略。
本页面最近更新:正在加载中,更新历史。
编辑页面:在 GitHub 上编辑此页!
本页面贡献者:RainPPR。